Πρόσθεση και αφαίρεση κλασμάτων - Μεικτοί αριθμοί

ΣΚΟΠΟΣ ΤΟΥ ΙΣΤΟΛΟΓΙΟΥ

Το συγκεκριμένο ιστολόγιο δημιουργήθηκε για να παρουσιάσει θεωρία και ασκήσεις πάνω στους μεικτούς αριθμούς αλλά και πάνω στην πρόσθεση και αφαίρεση κλασμάτων. Μετά από κάθε κομμάτι θεωρίας θα υπάρχουν παραδείγματα ώστε να κατανοήσετε καλύτερα την θεωρία αλλά και ασκήσεις που θα πρέπει να κάνετε. Επίσης θα συναντήσουμε ασκήσεις αντιστοίχισης και πολλαπλής επιλογής όπου μέσα από τη συμμετοχή σας, θα ελέγξετε τι θυμάστε από όσα είπαμε στο μάθημα. Ακόμα θα κάνετε ένα φύλλο εργασίας το οποίο περιέχει μία άσκηση αντιστοίχισης και μία ομαδική άσκηση την οποία θα κάνετε αφού χωριστείτε σε ομάδες. Η ομαδική εργασία έχει σκοπό να συνεργαστείτε ομαδικά με τους συμμαθητές σας ώστε να ανταλλάξετε ιδέες και απόψεις. Ακόμα υπάρχουν κάποια βίντεο ως επιπλέον βοήθεια για όποιον την χρειάζεται τα οποία περιέχουν θεωρία αλλά και ασκήσεις για παραπάνω εξάσκηση. Επίσης μπορούμε να γράφουμε σχόλια ή παρατηρήσεις όπου πιστεύουμε ότι χρειάζεται κατά τη διάρκεια του μαθήματος.

ΕΠΙΠΛΕΟΝ ΥΛΙΚΟ

• Στο παρακάτω βίντεο υπάρχουν επιπλέον ασκήσεις πάνω στους μεικτούς                   αριθμούς για μεγαλύτερη κατανόηση

 

• Στο παρακάτω βίντεο υπάρχουν επιπλέον ασκήσεις πάνω στην πρόσθεση και           αφαίρεση κλασμάτων για εξάσκηση

 

ΘΕΩΡΙΑ ΚΑΙ ΑΣΚΗΣΕΙΣ ΣΤΗΝ ΠΡΟΣΘΕΣΗ ΚΑΙ ΑΦΑΙΡΕΣΗ ΚΛΑΣΜΑΤΩΝ

• Πρόσθεση και αφαίρεση ομώνυμων κλασμάτων

1. Για να προσθέσουμε δύο ή περισσότερα ομώνυμα κλάσματα, προσθέτουμε τους     αριθμητές τους και κρατάμε τον κοινό τους παρονομαστή.

Παράδειγμα

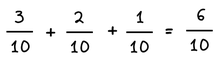
2. Για να αφαιρέσουμε δύο ή περισσότερα ομώνυμα κλάσματα, αφαιρούμε τους                   αριθμητές τους και κρατάμε τον κοινό τους παρονομαστή .

Παράδειγμα

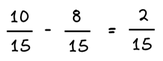
Άσκηση 1

Να κάνετε την παρακάτω άσκηση αντιστοίχισης

 

• Πρόσθεση και αφαίρεση ετερώνυμων κλασμάτων

1. Για να προσθέσουμε δύο ή περισσότερα ετερώνυμα κλάσματα, τα μετατρέπουμε       πρώτα σε ομώνυμα και στη συνέχεια προσθέτουμε τα ομώνυμα κλάσματα.
2. Για να αφαιρέσουμε δύο ή περισσότερα ετερώνυμα κλάσματα, τα μετατρέπουμε       πρώτα σε ομώνυμα και στη συνέχεια αφαιρούμε τα ομώνυμα κλάσματα.

Παρατήρηση: Για να θυμηθώ πως βρίσκω το Ελάχιστο Κοινό Πολλαπλάσιο (Ε.Κ.Π.) το οποίο θα μου χρειαστεί για να κάνω δύο ή περισσότερα κλάσματα ομώνυμα, μπορώ να παρακολουθήσω το παρακάτω βίντεο

          

Παράδειγμα

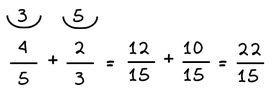
Άσκηση 2

Να αντιστοιχήσετε τις πράξεις στην πρώτη στήλη με τα αποτελέσματα στην δεύτερη

6/8 + 2/4	2/42
5/6 + 14/6	6/36
8/6 - 9/7	19/6
12/36 - 1/6	1
1/4 + 2/3 + 1/12	10/8

 

ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ

Άσκηση 1

Αφού χωριστείτε σε ομάδες, να κάνετε την παρακάτω άσκηση:

Ένας εργάτης σκάβει έναν κήπο σε 6 ώρες, ενώ ένας άλλος σκάβει τον ίδιο κήπο σε 5 ώρες. Τι μέρος του κήπου θα σκάψουν σε 1 ώρα αν δουλέψουν και οι δύο μαζί.

 

Άσκηση 2

Η παρακάτω άσκηση είναι άσκηση αντιστοίχησης πάνω σε αυτά που είδαμε στο συγκεκριμένο μάθημα

https://quizlet.com/829269026/match?funnelUUID=128f3255-ba1a-4305-8b99-ceb602499d92

 

 

ΘΕΩΡΙΑ ΚΑΙ ΑΣΚΗΣΕΙΣ ΜΕΙΚΤΩΝ ΑΡΙΘΜΩΝ

• Μεικτός αριθμός 

Το άθροισμα ενός φυσικού αριθμού α με ένα κλάσμα β/γ ( συνήθως μικρότερο του 1), αντί να το γράψουμε α + β/γ, μπορούμε να το γράψουμε πιο απλά α β/γ. Δηλαδή:              α + β/γ = α β/γ.

Για να μετατρέψουμε ένα μεικτό αριθμό σε κλάσμα, αντί να κάνουμε κανονικά την πρόσθεση α + β/γ (αφού α β/γ = α + β/γ), μπορούμε να ακολουθήσουμε την διαδικασία που περιγράφει το παρακάτω παράδειγμα.

Παράδειγμα 1    

 

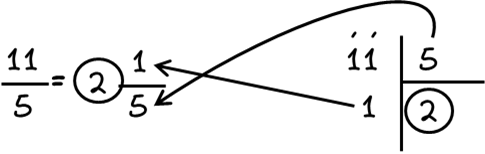
• Μετατροπή ενός κλάσματος σε μεικτό αριθμό

Για να μετατρέψουμε ένα κλάσμα σε μεικτό αριθμό, ακολουθούμε την διαδικασία που περιγράφει το παρακάτω παράδειγμα

Παράδειγμα 2

Άσκηση 1(Να επιλέξετε την σωστή απάντηση)

Ο μεικτός αριθμός 7 3/4 είναι ίσος με το κλάσμα:

α. 10/3         β. 5/3         γ. 28/4

 

Άσκηση 2 (Να επιλέξετε τη σωστή απάντηση)

Με ποιόν μεικτό αριθμό είναι ίσο το κλάσμα 5/2:

α. 2 1/2         β. 3 1/2         γ. 2 1/3