Όταν ολοκληρώσεις το μάθημα αυτό θα μπορείς:
• Να εξηγείς πώς παριστάνονται οι αριθμοί στο δυαδικό σύστημα αρίθμησης.
• Να εξηγείς πώς παριστάνονται οι αριθμοί στο δεκαεξαδικό σύστημα αρίθμησης.
• Να μετατρέπεις αριθμούς από το ένα σύστημα αρίθμησης στο άλλο
Όπως μάθαμε στο προηγούμενο μάθημα όλες οι πληροφορίες στον υπολογιστή παριστάνονται με τη χρήση ενός δυαδικού κώδικα. Παριστάνονται
δηλαδή με 0 και 1. Έτσι λοιπόν οι αριθμητικές πράξεις που κάνουν οι
υπολογιστές θα πρέπει να γίνονται στο δυαδικό σύστημα αρίθμησης. Για
παράδειγμα, όταν εμείς δίνουμε εντολή στον υπολογιστή να κάνει την
πράξη 8 + 5 = 13, συμβαίνουν τα παρακάτω:
Α. Οι δεκαδικοί αριθμοί 8 και 5 που εισάγουμε από το πληκτρολόγιο στον
υπολογιστή μετατρέπονται στους αντίστοιχους δυαδικούς αριθμούς.
Β. Ο υπολογιστής κάνει την πράξη στο δυαδικό σύστημα, βάσει του οποίου
λειτουργεί.
Γ. Το αποτέλεσμα της πρόσθεσης που είναι στο δυαδικό σύστημα μετατρέπεται στο δεκαδικό σύστημα και εμφανίζεται στην οθόνη του υπολογιστή.
Από τα παραπάνω φαίνεται η αναγκαιότητα της μετατροπής από το
δεκαδικό στο δυαδικό σύστημα και αντίστροφα.
Αριθμητικά συστήματα
Το σύστημα που μέχρι σήμερα έχετε χρησιμοποιήσει είναι το δεκαδικό, το
οποίο έχει τα εξής δέκα (10) σύμβολα: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Η βάση
αυτού του συστήματος λέμε ότι είναι το 10.
Επιτρεπτοί αριθμοί σε αυτό το σύστημα αρίθμησης είναι οι 123, 12,
981, 902, όχι όμως και οι 12Α, AF, 4F αφού οι αριθμοί αυτοί περιέχουν
και άλλα σύμβολα εκτός των 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Η τιμή ενός αριθμού π.χ. του 981 στο δεκαδικό σύστημα υπολογίζεται
ως εξής:
981 = 9·102 + 8·101 + 1·100 = 900 + 80 + 1
Ο υπολογιστής χρησιμοποιεί το δυαδικό σύστημα αρίθμησης το οποίο
έχει τα εξής δύο σύμβολα: 0,1. Η βάση αυτού του συστήματος λέμε ότι
είναι το 2.
Επιτρεπτοί αριθμοί σε αυτό το σύστημα αρίθμησης είναι οι 101,
101011, 110011, όχι όμως και οι 12, 31, 10812, αφού οι αριθμοί αυτοί
περιέχουν και άλλα σύμβολα εκτός των 0,1.
Η τιμή ενός αριθμού, π.χ. του 101 και του 1110, στο δυαδικό σύστημα
υπολογίζονται ως εξής:
101 = 1·22 + 0·21 + 1·20 = 4 + 0 + 1 = 5
1110 = 1·23 + 1·22 + 1·2 + 0·20 = 8 + 4 + 2 + 0 = 14
Υπάρχουν και άλλα συστήματα αρίθμησης όπως το οκταδικό σύστημα
αρίθμησης το οποίο έχει τα εξής οκτώ (8) σύμβολα: 0, 1, 2, 3, 4, 5, 6, 7.
Η βάση αυτού του συστήματος λέμε ότι είναι το 8.
Επιτρεπτοί αριθμοί σε αυτό το σύστημα αρίθμησης είναι οι 101,
101011, 123, 7501, όχι όμως και οι 81, 189, αφού οι αριθμοί αυτοί
περιέχουν και άλλα σύμβολα εκτός των 0, 1, 2, 3, 4, 5, 6, 7.
Η τιμή ενός αριθμού, π.χ. του 351, στο οκταδικό σύστημα υπολογίζεται
ως εξής:
351 = 3·82 + 5·81 + 1·80 = 192 + 40 + 1 = 233
Ακόμα υπάρχει και το δεκαεξαδικό σύστημα αρίθμησης το οποίο έχει
δεκαέξι σύμβολα. Επειδή δεν υπάρχουν περισσότερα από δέκα διαθέσιμα
αριθμητικά σύμβολα, χρησιμοποιούνται και οι χαρακτήρες A,B,C,D,E,F.
Έτσι λοιπόν τα σύμβολα του δεκαεξαδικού συστήματος είναι τα: 0, 1, 2,
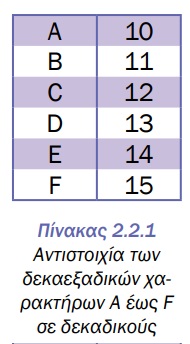
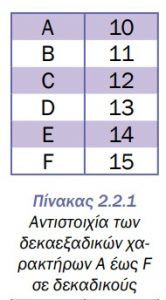
3, 4, 5, 6, 7, 8, 9, Α, Β, C, D, Ε, F. Το σύμβολο Α αντιπροσωπεύει το 10,
το Β αντιπροσωπεύει το 11, … το F αντιπροσωπεύει
το 15. Η βάση αυτού του συστήματος λέμε ότι είναι
το 16. Η αντιστοιχία των δεκαεξαδικών χαρακτήρων
(Α έως F) φαίνεται στον Πίνακα 2.2.1.
Παραδείγματος χάρη το 1Α του δεκαεξαδικού συστήματος αντιπροσωπεύει το 26 του δεκαδικού, το
FA αντιπροσωπεύει το 250. (Αμέσως παρακάτω θα
δούμε πώς θα μετατρέπουμε αριθμούς του δεκαεξαδικού συστήματος σε ισοδύναμους του δεκαδικού).
Παραδεκτοί αριθμοί σε αυτό το σύστημα αρίθμησης είναι οι 10, 101011, 123, 12, 8F1, 981,
12Β, AF, 4D, όχι όμως και οι 12G, ACR αφού οι αριθμοί αυτοί περιέχουν και άλλα σύμβολα εκτός των 0,
1, 2, 3, 4, 5, 6, 7, 8, 9, Α, Β, C, D, Ε, F.
Αφιερώστε 10:33΄από τον χρόνο σας και παρακολουθείστε το οπτικοακουστικό υλικό στο σύνδεσμο YouTube, για την μετατροπή από δυαδικό σε δεκαδικό.