1.4 Πυθαγόρειο Θεώρημα

Αυτή τη χρονιά θα ασχοληθούμε αρκετά με τα τρίγωνα και κυρίως με τα ορθογώνια τρίγωνα. Πάμε να τα γνωρίσουμε λίγο καλύτερα;

Ορθογώνιο τρίγωνο ονομάζεται το τρίγωνο που έχει μια ορθή γωνία (δηλαδή μια γωνία 90º).

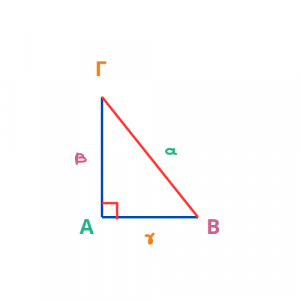Υπενθυμίζουμε ότι το ορθογώνιο τρίγωνο έχει τρεις πλευρές, οι οποίες ονομάζονται με δύο τρόπους:

• από τα ευθύγραμμα τμήματα ΑΒ, ΑΓ και ΒΓ
• από την απέναντι γωνία, χρησιμοποιώντας το αντίστοιχο μικρό γράμμα, δηλαδή
  • • απέναντι από τη γωνία Α βρίσκεται η πλευρά α
    • απέναντι από τη γωνία Β βρίσκεται η πλευρά β και
    • απέναντι από τη γωνία Γ βρίσκεται η πλευρά γ.

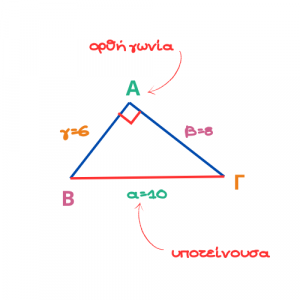
Η πλευρά που βρίσκεται απέναντι από την ορθή γωνία είναι η μεγαλύτερη πλευρά του ορθογωνίου τριγώνου και ονομάζεται υποτείνουσα.

Οι άλλες δύο πλευρές ονομάζονται κάθετες πλευρές.

---

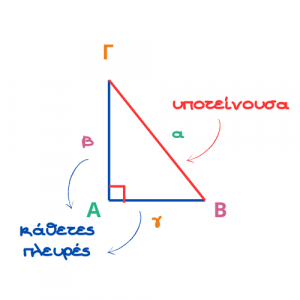
Πυθαγόρειο Θεώρημα

Ένα από τα πιο αγαπητά θεωρήματα των μαθηματικών είναι το Πυθαγόρειο Θεώρημα. Και αν δε με πιστεύετε, δείτε το παρακάτω βίντεο.

Είναι τόσο διάσημο, που έχει γίνει και τραγούδι!!!!

"Σε κάθε ορθογώνιο τρίγωνο το άθροισμα των τετραγώνων των δύο κάθετων πλευρών είναι ίσο με το τετράγωνο της υποτείνουσας."

Και τι εννοεί ο Πυθαγόρας με αυτό;

Παρατηρήστε την παρακάτω φωτογραφία.

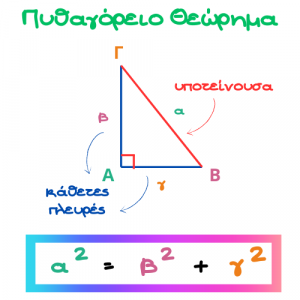
Το Πυθαγόρειο θεώρημα το χρησιμοποιούμε όταν γνωρίζουμε τις δύο πλευρές ενός ορθογωνίου τριγώνου και θέλουμε να βρούμε την τρίτη πλευρά.

Πάμε να το δούμε αναλυτικά μέσα από παραδείγματα.

Α' Περίπτωση: Ξέρω τις δύο κάθετες πλευρές και ψάχνω να βρω την υποτείνουσα.

Παίρνω τον τύπο, κάνω αντικατάσταση στις κάθετες πλευρές και κάνω πράξεις.

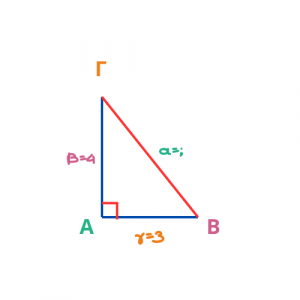Εφαρμόζω Πυθαγόρειο Θεώρημα στο τρίγωνο ΑΒΓ και έχω:

α² = β²+γ²

ΒΓ² = ΑΓ²+ΑΒ²

α² = 4²+3²

α² = 16+9

α² = 25

α = 5

Β' Περίπτωση: Ξέρω την υποτείνουσα και τη μια κάθετη πλευρά και ψάχνω να βρω την άλλη κάθετη πλευρά.

Α' τρόπος: Παίρνω τον τύπο, κάνω αντικατάσταση την υποτείνουσα και λύνω εξίσωση.

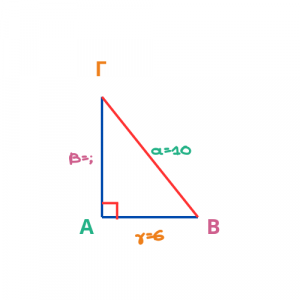
Εφαρμόζω Πυθαγόρειο Θεώρημα στο τρίγωνο ΑΒΓ και έχω:

α² = β²+γ²

ΒΓ² = ΑΓ²+ΑΒ²

10² = β²+6²

100 = β²+36

β² = 100-36

β² = 64

β=8

Β' Τρόπος: Ξεκινάω από την πλευρά που ψάχνω, δηλαδή την κάθετη.

κάθετη² = υποτείνουσα² - κάθετη²

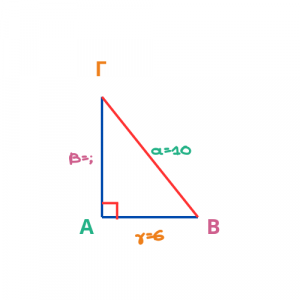
β² = α² - γ²

ΑΓ² = ΒΓ² - ΑΒ²

β² = 10²-6²

β²=100-36

β² = 64

β=8

Για να εμβαθύνουμε λίγο περισσότερο στο Πυθαγόρειο Θεώρημα, ας παρακολουθήσουμε το παρακάτω βίντεο, στο οποίο αναφέρονται δύο αποδείξεις του θεωρήματος.

---

Αντίστροφο Πυθαγορείου Θεωρήματος

"Αν σε ένα τρίγωνο, το τετράγωνο της μεγαλύτερης πλευράς είναι ίσο με το άθροισμα των τετραγώνων των δύο άλλων πλευρών, τότε η γωνία που βρίσκεται απέναντι από τη μεγαλύτερη πλευρά είναι ορθή."

Και σε τι μου χρησιμεύει αυτό;

Το αντίστροφο του Πυθαγορείου Θεωρήματος το χρησιμοποιούμε όταν γνωρίζουμε και τις 3 πλευρές ενός τριγώνου και θέλουμε να δείξουμε ότι το τρίγωνο είναι ορθογώνιο.

Ας δούμε ένα παράδειγμα:

Θέλουμε να εξετάσουμε αν το παρακάτω τρίγωνο είναι ορθογώνιο.

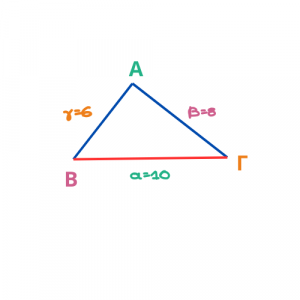
Εφαρμόζω Αντίστροφο Πυθαγόρειο Θεώρημα στο τρίγωνο ΑΒΓ και έχω:

Παίρνω τη μεγαλύτερη πλευρά στο τετράγωνο:

α² = ΒΓ²=10²=100

Παίρνω το άθροισμα των τετραγώνων των δύο άλλων πλευρών:

β²+γ² = ΑΓ²+ΑΒ² = 8²+6² = 64+36=100

Άρα ισχύει α² = β²+γ². Οπότε το τρίγωνο είναι ορθογώνιο με υποτείνουσα την πλευρά α (τη μεγαλύτερη πλευρά) και ορθή γωνία τη γωνία Α.

Πάμε να τα συνοψίσουμε όλα αυτά στο παρακάτω βίντεο.