Updated on 11 gruodžio, 2023
Βίντεο_ Πως μέτρησε ο Θαλής το ύψος της πυραμίδας του Χέοπα.
Ο συνάδελφος μαθηματικός Μόσχος Αλέξανδρος έχει δημιουργήσει ένα βίντεο, στο οποίο παρουσιάζει πως ο Θαλής χρησιμοποίησε την ομοιότητα τριγώνων για να υπολογίσει το ύψος της Πυραμίδας του Χέοπα. Για να το παρακολουθήσετε ακολουθήστε τον παρακάτω σύνδεσμο: https://www.youtube.com/watch?v=AwZJAcQLocU
Updated on 11 gruodžio, 2023
2. Περιεχόμενα Ιστολογίου
Το παρόν ιστολόγιο περιλαμβάνει τις κατηγορίες:
Εισαγωγή: Παρουσιάζεται ο σκοπός κι η παιδαγωγική αξία του περιεχομένου του ιστολογίου, καθώς και τα περιεχόμενα αυτού.
Βίντεο: Παρατίθενται τρία βίντεο με σκοπό την πρόκληση ενδιαφέροντος αρχικά και στη συνέχεια την παρατήρηση και την ανακάλυψη της πληροφορίας που περιέχει.
Θεωρία: Έχει ένα παράδειγμα, χρησιμοποιώντας διαδικασίες μαθησιακής υποστήριξης με αλληλεπίδραση, όπου οι μαθητές συγκρίνουν δύο τρίγωνα με σκοπό να τα δείξουν όμοια.
Ερωτήσεις κατανόησης: Περιέχει ερωτήσεις που βασίζονται σε απλή εφαρμογή της θεωρίας του μαθήματος και ερωτήσεις αυτοαξιολόγησης.
Ασκήσεις: Ασκήσεις με πραγματικό ή μη ενδιαφέρον για εξάσκηση και εφαρμογή της γνώσης που αποκτήθηκε.
Ομαδικές εργασίες: Σε ομάδες θα εργαστείτε σε δύο εργασίες. Η μία αφορά ένα μικροπείραμα του δυναμικού λογισμικού Geogebra και η δεύτερη τον αρχαίο Έλληνα μαθηματικό Θαλή το Μιλήσιο.
Ασκήσεις μέσα από εκπαιδευτικό λογισμικό: Θα εργαστείτε σε 2 μικροπειράματα, αλληλοεπιδρώντας με τα εκπαιδευτικά λογισμικά Χελωνόσφαιρα και Geogebra.
Κατασκευές: Προαιρετική δημιουργία 2 κατασκευών χρήση της ομοιότητας σχημάτων, ενός παντογράφου και τον κάνναβο του σχεδιαστή.
Πόροι και Υπερσύνδεσμοι: Παρατίθενται βιβλία και ιστότοποι, χρήσιμα για τις έρευνές σας, τις εργασίες σας, την καλύτερη κατανόηση του γνωστικού αντικειμένου και τον εμπλουτισμό των γνώσεών σας.
Posted on 10 gruodžio, 2023
Ο κάνναβος του σχεδιαστή
Ο Αλφρεντ Ντύρερ (1471-1528) στο βιβλίο του “Πραγµατεία επί των µετρήσεων” (1525 και
1538) περιείχε εικονογραφήσεις προοπτικών βοηθηµάτων,
όπως ο κάνναβος του σχεδιαστή. Με το εργαλείο αυτό
ο καλλιτέχνης µπορούσε να σχεδιάζει µε µεγάλη ακρίβεια
εικόνες εκ του φυσικού σε σµίκρυνση.
Ο κάνναβος δεν είναι παρά ένα ξύλινο πλαίσιο στο οποίο είναι
στερεωµένες µαύρες κλωστές καλά τεντωµένες, ώστε να
σχηµατίζουν ένα τετραγωνισµένο πλαίσιο.

Ένα στόχαστρο τοποθετείται πάνω στο τραπέζι σχεδίασης σε
απόσταση διπλάσια από το ύψος του πλαισίου. Ο καλλιτέχνης
παρατηρεί από την τρύπα του στροχάστρου και σχεδιάζει το
περίγραµµα του µοντέλου σε µια τετραγωνισµένη επιφάνεια. Για να επιτύχει την έντονη
σµίκρυνση της στάσης τοποθετεί τον κάνναβο πολύ κοντά στο µοντέλο.

Μπορείτε να φτιάξετε από χαρτόνι ή ξύλο ένα κάνναβο και τοποθετώντας το
πάνω σ’ ένα τραπέζι µπροστά από µερικά αντικείµενα να σχεδιάσουν σε τετραγωνισµένο
χαρτί το περίγραµµά τους. Στη συνέχεια επιστρατεύοντας το ταλέντο σας να ολοκληρώσετε
τη σύνθεση.
Βιβλιογραφία
– AlisonCole: Ανακαλύπτω την τέχνη-Προοπτική, εκδόσεις Δεληθανάση-Ερευνητές,
Αθήνα 1993.
– Carol Vorderman: Ανακαλύπτω τα Μαθηµατικά, εκδόσεις Ερευνητές, Αθήνα 1998.
Updated on 10 gruodžio, 2023
Φτιάξτε έναν παντογράφο
Ο παντογράφος είναι ένα όργανο µε το οποίο oι σχεδιαστές έφτιαχναν σχέδια σε µεγέθυνση ή σµίκρυνση. Σήµερα µε τη χρήση των φωτοτυπικών µηχανηµάτων και των υπολογιστών έχει περιπέσει σε αχρηστία. Εξακολουθούν όµως να τον χρησιµοποιούν όσοι σχεδιάζουν µε το χέρι καθώς και εκείνοι που φτιάχνουν µινιατούρες. Για την κατασκευή ενός αυτοσχέδιου παντογράφου χρειάζονται κοµµάτια σκληρού χαρτονιού ή ξύλου (π.χ δυο κοµµάτια των 22cm και άλλα δυο των 12cm) παξιµάδια και βίδες και ένας φελλός. Σε όλα τα κοµµάτια του ξύλου κάνουµε 5 τρύπες σε ίσες αποστάσεις αφήνοντας περιθώριο 1cm από κάθε άκρη. Συναρµολογούµε στη συνέχεια τα διάφορα τµήµατα του οργάνου, όπως φαίνεται στην εικόνα.
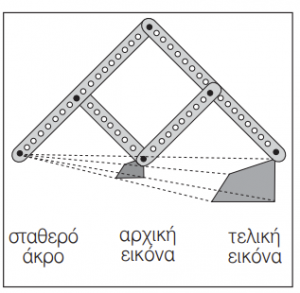
Κρατώντας σταθερό µε το ένα χέρι το ένα άκρο του παντογράφου, διατρέχουµε το περίγραµµα της εικόνας µε το άλλο και το µολύβι σχεδιάζει τη µεγέθυνση ή τη σµίκρυνση της εικόνας. Στην εικόνα το σχέδιο που θα προκύψει θα είναι µια µεγέθυνση στο διπλάσιο. Αν συνδέσουµε σε διαφορετικά σηµεία τα µικρότερα µε τα µεγαλύτερα κοµµάτια του ξύλου, µπορούν να σχεδιαστούν µικρότερα ή µεγαλύτερα σχέδια. Στις ιστοσελίδες της Εκπαιδευτικής Πύλης του ΥΠΕΠΘ www.e-yliko.gr υπάρχει µια προσοµοίωση ενός παντογράφου µε τον οποίο οι µαθητές µπορούν να σχεδιάσουν ένα σχήµα και να δουν ταυτόχρονα να σχηµατίζεται µια µεγέθυνση ή µια σµίκρυνσή του. Το ίδιο και στην ιστοσελίδα http://www.ies.co.jp/math/java/geo/panta/panta.html
Posted on 10 gruodžio, 2023
Άσκηση 4
 |
Ένα ζωγράφος δοκιμάζει να ζωγραφίσει τον κεκλιμένο πύργο της Πίζας. Το ύψος του πύργου είναι 60 m και το ύψος που έχει τώρα, λόγω της απόκλισης από την κατακόρυφη, είναι 59,8m. Στο σχέδιό του το ύψος του πύργου θέλει να είναι 30 cm. Αν εσύ ήσουν ο ζωγράφος πόσο θα σχεδίαζες το κατακόρυφο ύψος; Πώς θα ήσουν σίγουρος ότι με αυτές τις διαστάσεις ο πύργος της ζωγραφιάς θα γέρνει όπως ο πύργος της Πίζας; |
Updated on 10 gruodžio, 2023
Άσκηση 1
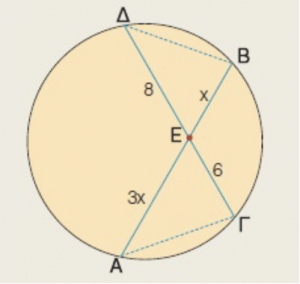 |
Να αποδείξετε το ότι τα τρίγωνα ΑΕΓ, ΒΕΔ είναι όμοια και να υπολογίσετε το x. Την απάντησής σας θα την γράψετε στα σχόλια. |
Updated on 10 gruodžio, 2023
Άσκηση 3
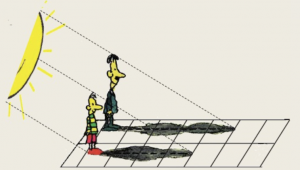
Εκφώνηση:
Ο γιος έχει ύψος 1,36 m. Ποιο είναι το ύψος του πατέρα του;
Η απάντησή σας, θα δοθεί στα σχόλια.
Posted on 9 gruodžio, 2023
Βιβλία που αφορούν τη γεωμετρία και τους πρωταγωνιστές της
-
Τίτλος Συγγραφέας Λίγα λόγια για το περιεχόμενο... Η ΑΦΥΠΝΙΣΗ ΤΗΣ ΕΠΙΣΤΗΜΗΣ
ΑΙΓΥΠΤΙΑΚΑ ΒΑΒΥΛΩΝΙΑΚΑ ΚΑΙ ΕΛΛΗΝΙΚΑ ΜΑΘΗΜΑΤΙΚΑ
B. L. VAN DER WAERDEN Η Αφύπνιση της Επιστήμης είναι ένα από τα πιο πολυδιαβασμένα βιβλία της ιστορίας των μαθηματικών. Γραμμένο αρχικά στα ολλανδικά (1950), μεταφράστηκε στα αγγλικά, στα γερμανικά και στα ρωσικά και έγινε πολύ σύντομα έργο αναφοράς και ένα από τα κλασικά συγγράμματα του κλάδου. Η επιτυχία του βιβλίου οφείλεται στο ότι συγκεντρώνει, συνοψίζει και ολοκληρώνει κατά τρόπο άρτιο, έγκυρο και εμπεριστατωμένο έναν τεράστιο όγκο ερευνών για την ιστορία των αιγυπτιακών, των βαβυλωνιακών και των ελληνικών μαθηματικών, που διεξήχθησαν κατά την περίοδο 1920 - 1950. Τα αποτελέσματα αυτών των ερευνών δεν είχαν συγκεντρωθεί ως τότε σ’ ένα βιβλίο, και το καθήκον αυτό το εκπληρώνει κατά τον καλύτερο τρόπο ο Wan der Waerden. Το βιβλίο αποτελείται από δύο μεγάλες ενότητες. Στην πρώτη ενότητα εξετάζονται τα αιγυπτιακά και τα βαβυλωνιακά μαθηματικά, δηλαδή οι δύο μεγάλες μαθηματικές παραδόσεις από τις οποίες άντλησαν, σύμφωνα με τον συγγραφέα, οι Έλληνες μαθηματικοί της πρώιμης εποχής. Το κύριο αντικείμενο του βιβλίου όμως είναι τα ελληνικά μαθηματικά, στην ιστορία των οποίων είναι αφιερωμένα τα πέντε κεφάλαια της δεύτερης ενότητας. ΕΥΚΛΕΙΔΗ "ΣΤΟΙΧΕΙΑ" Κέντρο Έρευνας Επιστήμης και Εκπαίδευσης (Κ.Ε.ΕΠ.ΕΚ.) Τα "Στοιχεία" του Ευκλείδη είναι χωρισμένα σε τρεις τόμους. Ο πρώτος τόμος περιλαμβάνει τα βιβλία 1 έως 6, ο δεύτερος τόμος τα βιβλία 7 έως 10 και ο 3ος τόμος τα βιβλία από 11 έως και 13. Η γεωμετρία του Ευκλείδη, όπως αυτή παρουσιάζεται στα "Στοιχεία", είναι ένα έργο πρωτοποριακό και υψηλού επιπέδου. Ο Ευκλείδης δημιούργησε ένα καταπληκτικό μαθηματικό σύστημα, το οποίο είναι το πρώτο αξιωματικό σύστημα που έγινε στην ιστορία της ανθρωπότητας και το οποίο λειτουργεί ακόμα και σήμερα με μερικές μόνο διαφοροποιήσεις. Η σύγχρονη απόδοσή του εμπεριέχει επεξηγήσεις και σχολιασμό. ΙΣΤΟΡΙΑ ΤΩΝ ΕΛΛΗΝΙΚΩΝ ΜΑΘΗΜΑΤΙΚΩΝ
ΠΡΩΤΟΣ ΤΟΜΟΣ_"ΑΠΟ ΤΟ ΘΑΛΗ ΣΤΟΝ ΕΥΚΛΕΙΔΗ"
ΔΕΥΤΕΡΟΣ ΤΟΜΟΣ_"ΑΠΟ ΤΟΝ ΑΡΙΣΤΑΡΧΟ ΣΤΟΝ ΔΙΟΦΑΝΤΟ"
Sir Thomas L. Heath Πράγματι, διαπιστώνοντας πως ένα τόσο μεγάλο μέρος της ελληνικής σκέψης αναφέρεται στα Μαθηματικά, μπορούμε να υποστηρίξουμε ότι, εάν θέλουμε να κατανοήσουμε πλήρως την ελληνική σκέψη είναι σκόπιμο να ξεκινήσουμε από τη γεωμετρία τους." Ό,τι έδωσε στο Sir Thomas Heath τη δυνατότητα κατανόησης της ελληνικής διάνοιας, δηλαδή η βαθιά εξοικείωση με τη γλώσσα, τη λογοτεχνία, τη φιλοσοφία, και το σύνολο των επιστημών, τον έφερε ίσως πιο κοντά στα αγαπημένα του θέματα και στα ιδεώδη των καλλιεργημένων ανθρώπων απ' ό,τι συνηθίζεται ή είναι δυνατόν στη σημερινή εποχή. Ο Heath διάβασε με κριτικό και σχολαστικό τρόπο τα πρωτότυπα κείμενα και παρουσίασε σε αυτό το δίτομο έργο την ενόραση ενός μαθηματικού σε συνδυασμό με τη σαφήνεια της κλασσικής αγγλικής γλώσσας. "Από όλες τις εκδηλώσεις της ελληνικής διάνοιας καμία δεν προκαλεί μεγαλύτερη εντύπωση και δέος από εκείνη που αποκαλύπτεται στην ιστορία των ελληνικών Μαθηματικών." Ο Heath καταγράφει αυτήν την ιστορία με την επιστημονική κατανόηση και περιεκτικότητα βάσει των οποίων το έργο αυτό θεωρείται σήμερα τόσο κλασικό, όσο ήταν και κατά την έκδοσή του το 1921. Η σύνδεση και η ενότητα μεταξύ Μαθηματικών και φιλοσοφίας, χαράσσουν το περίγραμμα της ιστορίας όπως παρουσιάζεται στο βιβλίο αυτό. Η ΓΕΩΜΕΤΡΙΑ και οι εργάτες της στην ΑΡΧΑΙΑ ΕΛΛΑΔΑ Δημήτρης Τσιμπουράκης Στο βιβλίο αυτό γίνεται μία προσπάθεια παρουσίασης εκείνων των μαθηματικών της ελληνικής αρχαιότητας, των οποίων τα έργα τους εξασφάλισαν μία μόνιμη θέση στην ιστορία του ανθρώπινου πολιτισμού. Ακόμα δίνεται ένα μέρος του έργου τους, συνοπτικά παρουσιασμένο αλλά αναγκαίο, για να γίνει αντιληπτή η συμβολή τους στην ίδρυση και εξέλιξη αυτής της εξαίσιας επιστήμης των μαθηματικών.

