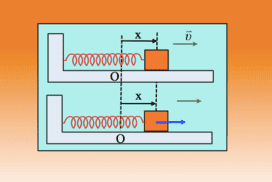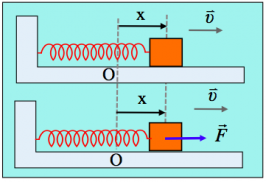
Ένα σώμα Σ είναι δεμένο στο άκρο ιδανικού ελατηρίου, εκτελώντας ΑΑΤ με εξίσωση απομάκρυνσης x=0,2∙ημ(6t) (μονάδες στο S.Ι.), σε λείο οριζόντιο επίπεδο, γύρω από τη θέση Ο, θέση φυσικού μήκους του ελατηρίου.
Το ίδιο σύστημα τίθεται σε εξαναγκασμένη ταλάντωση, με την επίδραση εξωτερικής περιοδικής δύναμης F, ενώ ταυτόχρονα δέχεται από το περιβάλλον του και δύναμη απόσβεσης της μορφής Fαπ=-bυ. Μετά την αποκατάσταση σταθερού πλάτους ταλάντωσης, γύρω από την ίδια θέση ισορροπίας Ο, λαμβάνοντας κάποια στιγμή ως αρχή μέτρησης του χρόνου, παίρνουμε την εξίσωση x=0,2∙ημ(5t) (S.Ι.), για την απομάκρυνση του σώματος.
Για μια θέση με απομάκρυνση x, όπου το σώμα κινείται προς τα δεξιά, όπως στο σχήμα:
i) Αν υ1 η ταχύτητα στην περίπτωση της ΑΑΤ και υ2 η ταχύτητα στην εξαναγκασμένη ταλάντωση, ισχύει:
α) υ1 < υ2, β) υ1 = υ2, γ) υ1 > υ2.
ii) Αν α1 και α2 οι αντίστοιχες επιταχύνσεις, τότε:
α) α1 < α2, β) α1 = α2, γ) α1 > α2.
iii) Σε ποια περίπτωση η δυναμική ενέργεια ταλάντωσης είναι μεγαλύτερη; Στην ΑΑΤ ή στην εξαναγκασμένη ταλάντωση, για την ίδια απομάκρυνση x;
Αν dU1/dt=λ και dU2/dt=μ οι αντίστοιχοι ρυθμοί μεταβολής της δυναμικής ενέργειας, ισχύει:
α) λ < μ, β) λ = μ, γ) λ > μ.
Να δικαιολογήσετε τις απαντήσεις σας.
ή