Δυνάμεις Ρητών Αριθμών με εκθέτη φυσικό

Για πάμε να εξερευνήσουμε ένα δύσκολο κομμάτι των μαθηματικών... Σας θυμίζει κάτι το 2³;

Τις δυνάμεις τις έχουμε συναντήσει στο Δημοτικό και στην αρχή της Α' Γυμνασίου. Πάμε να θυμηθούμε, όμως, τι είναι οι δυνάμεις και τι γνωρίζουμε για αυτές. Ας δούμε πρώτα ένα παράδειγμα.

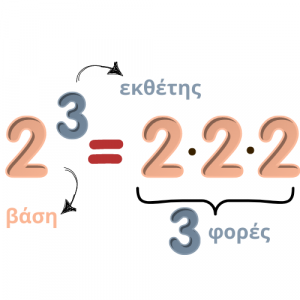
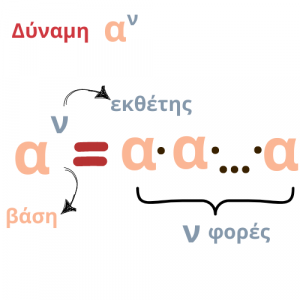
Δύναμη

Η γενική της μορφή είναι :

Υπενθύμιση:

• Η δύναμη α^ν διαβάζεται νιοστή δύναμη του α ή α στη ν.
• Η δύναμη α² διαβάζεται α στη δευτέρα ή α στο τετράγωνο ή τετράγωνο του α.
• Η δύναμη α³ διαβάζεται α στην τρίτη ή α στον κύβο ή κύβος του α.

Συχνό Λάθος:

Εδώ χρειάζεται ιδιαίτερη προσοχή, ώστε να μην υπολογίζετε τη δύναμη ως πολλαπλασιασμό. Δηλαδή:

2³=2•3=6   Αυτό είναι ΛΑΘΟΣ!!!! Το σωστό είναι: 2³=2•2•2=8.

Ιδιότητες Ορισμού:

• α¹=α
• 1^ν=1
• 0⁰ δεν ορίζεται
• α⁰=1 , όπου α≠0

Πρόσημο Δύναμης

Καλό το 2³ αλλά τι γίνεται με το -2³;

και όχι μόνο αυτό... Αλήθεια, τι θα κάνατε σε καθεμία από τις παρακάτω περιπτώσεις;

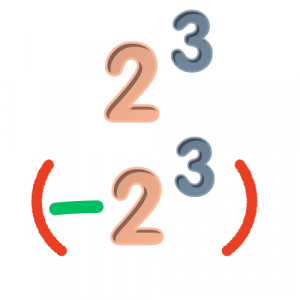
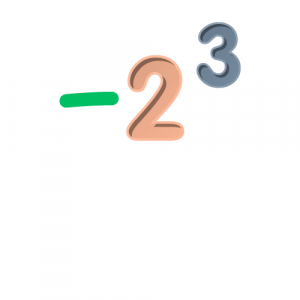
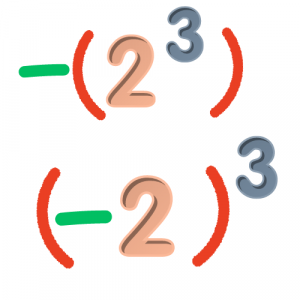
Ο γενικός κανόνας υπολογισμού των δυνάμεων είναι ίδιος και στην περίπτωση που έχουμε πρόσημα. Αυτό που πρέπει να ξεχωρίσετε σε πρώτη φάση είναι πότε ο εκθέτης επηρεάζει το πρόσημο και πότε όχι, με άλλα λόγια ποια είναι η βάση της δύναμης.

 

 

εδώ η βάση της δύναμης είναι το 2, οπότε ο εκθέτης επηρεάζει μόνο το 2 και όχι το -.

 

 

 

εδώ η βάση της δύναμης είναι το 2, οπότε ο εκθέτης επηρεάζει μόνο το 2 και όχι το -.

 

εδώ η βάση της δύναμης είναι το -2, οπότε ο εκθέτης επηρεάζει και το πρόσημο και το 2.

 

 

 

 

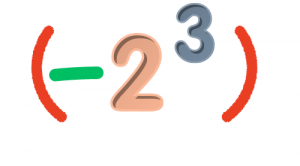
εδώ η βάση της δύναμης είναι το 2, οπότε ο εκθέτης επηρεάζει μόνο το 2 και όχι το -.

 

 

• Όταν η βάση είναι θετικός αριθμός υπολογίζουμε τις δυνάμεις, όπως ήδη ξέρουμε, και το αποτέλεσμα βγαίνει πάντα θετικός αριθμός. Τι γίνεται, όμως, όταν η βάση είναι αρνητικός αριθμός;

Παρατηρείστε καλά τις παρακάτω φωτογραφίες και προσπαθήστε να καταλήξετε σε κάποιο συμπέρασμα.

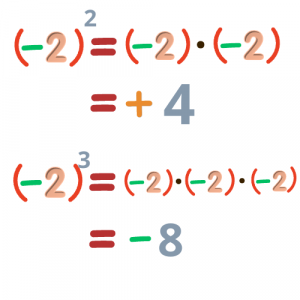
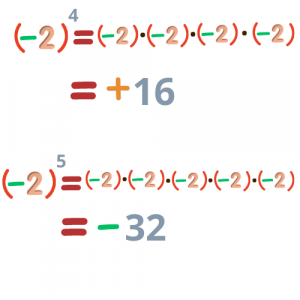
Παρατηρούμε ότι όταν η βάση είναι αρνητικός αριθμός, το αποτέλεσμα δεν είναι πάντα αρνητικό. Μπορείτε να καταλάβετε πότε είναι θετικός και πότε αρνητικός αριθμός το αποτέλεσμα;

Το πρόσημο εξαρτάται από τον εκθέτη και συγκεκριμένα:

• όταν ο εκθέτης είναι άρτιος / ζυγός αριθμός (2, 4, 6,...) το αποτέλεσμα βγαίνει θετικός αριθμός
• όταν ο εκθέτης είναι περιττός / μονός αριθμός (1, 3, 5,...) το αποτέλεσμα βγαίνει αρνητικός αριθμός.

 

Δυνάμεις Ρητών με εκθέτη φυσικό αριθμό

 

 

Ιδιότητες Πράξεων

Ίδια βάση	Κανόνας	Παράδειγμα
Πολλαπλασιασμός	αν•αμ=αν+μ	23•25=23+5=28
Διαίρεση	αν:αμ=αν-μ	35:32=35-2=33
	αν/αμ=αν-μ	35/32=35-2=33
Ίδιος εκθέτης
Πολλαπλασιασμός	αν•βν=(α•β)ν	23•53=(2•5)3=103
Διαίρεση	αν:βν=(α:β)ν	103:53=(10:5)3=23
	αν/βν=(α/β)ν	103/53=(10/5)3=23
Δύναμη σε δύναμη	(αν)μ=αν•μ	(23)4=23•4=212

Παρατηρήσεις:

1. Οι ιδιότητες δυνάμεων ισχύουν μόνο στις πράξεις του πολλαπλασιασμού και της διαίρεσης. Στην πρόσθεση και στην αφαίρεση ακολουθούμε την προτεραιότητα των πράξεων, όπως στο παράδειγμα 2³+2⁴=8+16=24.
2. Αυτό που είναι ίδιο (βάση ή εκθέτης) μένει ίδιο.
3.  Οι ιδιότητες δυνάμεων ισχύουν και αντίστροφα.
4.  Προσπαθήστε να ξεχωρίσετε την πρώτη και την τελευταία ιδιότητα!

 

 

Ασκήσεις στις Δυνάμεις με εκθέτη φυσικό αριθμό