Updated on October 29, 2024
1.5. Χαρακτήρες Διαιρετότητας – ΜΚΔ – ΕΚΠ – Ανάλυση Αριθμού σε γινόμενο πρώτων παραγόντων
Πολλαπλάσια
Πολλαπλάσια ενός φυσικού αριθμού α είναι οι αριθμοί που προκύπτουν από τον πολλαπλασιασμό του με όλους τους φυσικούς αριθμούς.
0, α, 2α, 3α, 4α, …
| Πολλαπλάσια του 3 |
| 0 · 3 = 0 |
| 1 · 3 = 3 |
| 2 · 3 = 6 |
| 3 · 3 = 9 |
| 4 · 3 = 12 |
| … |
Με απλά λόγια είναι τα αποτελέσματα της προπαίδειας.
Ιδιότητες:
- Κάθε φυσικός αριθμός διαιρεί τα πολλαπλάσιά του.
π.χ. Το 4 είναι πολλαπλάσιο του 2, οπότε το 2 διαιρεί το 4.
- Κάθε φυσικός που διαιρείται από έναν άλλο είναι πολλαπλάσιό του.
π.χ. Το 6 διαιρείται από το 3. Οπότε το 6 είναι πολλαπλάσιο του 3.
- Αν ένας φυσικός διαιρεί έναν άλλο, θα διαιρεί και τα πολλαπλάσιά του.
π.χ. Το 2 διαιρεί το 6. Το 12 είναι πολλαπλάσιο του 6. Άρα το 2 διαιρεί το 12.
- Τα πολλαπλάσια ενός αριθμού είναι άπειρα.
- Με εξαίρεση το 0 και τον ίδιο τον αριθμό, όλα τα υπόλοιπα πολλαπλάσια είναι μεγαλύτερα από τον αριθμό.
Κοινά πολλαπλάσια του α και του β ονομάζονται οι αριθμοί που είναι συγχρόνως πολλαπλάσια του α και του β.
π.χ.
| 2 | 0,2,4,6,8,10,12,14,16,18,20,22,24,26,28,30,… |
| 5 | 0,5,10,15,20,25,30,35,40,45,50,55,60,65,70,… |
Οι αριθμοί 0,10,20,30 είναι πολλαπλάσια και του 2 και του 5, δηλαδή είναι τα κοινά τους πολλαπλάσια.
Ελάχιστο κοινό πολλαπλάσιο του α και του β ονομάζεται το μικρότερο μη μηδενικό κοινό πολλαπλάσιο του α και του β και συμβολίζεται με ΕΚΠ(α,β).
π.χ. Στο προηγούμενο παράδειγμα, το μικρότερο μη μηδενικό πολλαπλάσιο του 2 και του 5 είναι το 10. Οπότε ΕΚΠ(2,5)=10.
Διαιρέτες
Διαιρέτες ενός φυσικού αριθμού α είναι όλοι οι αριθμοί που τον διαιρούν.
- Κάθε αριθμός α έχει διαιρέτες τους αριθμούς 1 και α.
- Οι διαιρέτες έχουν πεπερασμένο πλήθος.
- Οι διαιρέτες ενός αριθμού είναι πάντα μικρότεροι ή ίσοι του αριθμού.
Πρώτος ονομάζεται ένας αριθμός (εκτός από το 1) που έχει διαιρέτες μόνο το 1 και τον εαυτό του.
π.χ. Οι αριθμοί 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 39, 41 κλπ διαιρούνται μόνο από το 1 και τον εαυτό τους. Άρα είναι πρώτοι.
Σύνθετος ονομάζεται ένας αριθμός που δεν είναι πρώτος.
π.χ. Ο αριθμός 4, εκτός από το 1 και το 4, έχει διαιρέτη και τον αριθμό 2. Άρα δεν είναι πρώτος, αλλά σύνθετος.
Το 1 δεν είναι ούτε πρώτος ούτε σύνθετος.
Κοινοί διαιρέτες των α και β ονομάζονται οι αριθμοί που είναι συγχρόνως διαιρέτες του α και του β.
π.χ.
| Δ6 | 1,2,3,6 |
| Δ15 | 1,3,5,15 |
Μέγιστος Κοινός Διαιρέτης των α, β ονομάζεται ο μεγαλύτερος από τους κοινούς διαιρέτες των α και β και συμβολίζεται με ΜΚΔ(α,β).
π.χ. Στο προηγούμενο παράδειγμα ο μεγαλύτερος κοινός διαιρέτης του 6 και του 15 είναι το 3. Οπότε ΜΚΔ(6,15)=3
- Δύο αριθμοί α και β ονομάζονται πρώτοι μεταξύ τους αν ισχύει ΜΚΔ(α,β)=1.
π.χ.
| Δ6 | 1,2,3,6 |
| Δ35 | 1,5,7,35 |
ΜΚΔ(6,35)=1 άρα οι αριθμοί 6 και 35 είναι πρώτοι μεταξύ τους.
Προσοχή! Οι έννοιες "πρώτο αριθμοί" και "πρώτοι μεταξύ τους" είναι διαφορετικοί!
Κριτήρια Διαιρετότητας
Τα κριτήρια διαιρετότητας είναι πολύ χρήσιμα, καθώς μας βοηθούν να επιλέγουμε τους κατάλληλους διαιρέτες. Στο παρακάτω αρχείο υπάρχουν αναλυτικά τα κριτήρια διαιρετότητας, τα οποία έχουν χωριστεί σε 3 κατηγορίες για τη διευκόλυνσή σας.
Ανάλυση σε γινόμενο πρώτων παραγόντων
Ανάλυση Αριθμού σε Γινόμενο Πρώτων Παραγόντων ονομάζεται η γραφή ενός φυσικού αριθμού ως γινόμενο πρώτων αριθμών.
Κάθε σύνθετος αριθμός μπορεί να αναλυθεί σε γινόμενο πρώτων παραγόντων κατά μοναδικό τρόπο.
Διαδικασία:
- Κάνουμε διαδοχικές διαιρέσεις.
- Σταματάμε όταν το τελευταίο πηλίκο είναι 1.
π.χ.
| 60 | 2 |
| 30 | 2 |
| 15 | 3 |
| 5 | 5 |
|
1 |
60 = 2 · 2 · 3 · 5
= 22 · 3 · 5
Εύρεση ΕΚΠ δύο ή περισσότερων αριθμών:
- Αναλύουμε τους αριθμούς σε γινόμενο πρώτων παραγόντων.
- Σχηματίζουμε το γινόμενο των κοινών και μη κοινών παραγόντων με το μεγαλύτερο από τους εκθέτες τους.
π.χ. ΕΚΠ(486000, 151200)
486000= 24 · 35 · 53
151200= 25 · 33 · 52 · 7
ΕΚΠ(486000, 151200) = 25 · 35 · 53 · 7
Εύρεση ΜΚΔ δύο ή περισσότερων αριθμών:
- Αναλύουμε τους αριθμούς σε γινόμενο πρώτων παραγόντων.
- Σχηματίζουμε το γινόμενο των κοινών παραγόντων με το μικρότερο από τους εκθέτες τους.
π.χ. ΜΚΔ(486000, 151200)
486000= 24 · 35 · 53
151200= 25 · 33 · 52 · 7
ΜΚΔ(486000, 151200) = 24 · 33 · 52
Προσοχή!
Στο Ελάχιστο Κ.Π. θέλουμε τη μεγαλύτερη δύναμη.
Στο Μέγιστο Κ.Π. θέλουμε τη μικρότερη δύναμη.
Updated on October 17, 2024
Α.1.1. Η έννοια της μεταβλητής – Αλγεβρικές Παραστάσεις
Καλώς ήρθατε στη χώρα των γραμμάτων!!!
Δικαίως θα αναρωτιέστε τώρα, τι σχέση έχουν τα γράμματα με τα μαθηματικά... Η απάντηση είναι ... μεγάλη! Είστε έτοιμοι για εξερεύνηση;;;
Το παρακάτω χιουμοριστικό βίντεο θα σας φέρει σε επαφή με το περιεχόμενο που θα διαπραγματευτούμε σε αυτήν την ενότητα.
Πηγή: daskalos98 (2011, Δεκέμβριος 2). Ο άγνΩστος Χ [Βίντεο]. YouTube. Ανακτήθηκε από https://www.youtube.com/watch?v=IgH06_8Nw6I
Ο πιο γνωστός άγνωστος στην ιστορία των μαθηματικών είναι ο άγνωστος x. Γιατί, όμως, συμβαίνει αυτό; Το παρακάτω βίντεο θα σας βοηθήσει να απαντήσετε σε αυτό το ερώτημα.
Πηγή: Ted. (2012, Ιούνιος 6). Why is 'x' the unknown?| Terry Moore [Video] YouTube. Ανακτήθηκε από https://www.youtube.com/watch?v=YX_OxBfsvbk
Τελικά, γιατί καθιερώθηκε ο άγνωστος x; Μπορείτε να μου γράψετε στα σχόλια τις απαντήσεις σας.
Η έννοια της μεταβλητής - Ορισμοί
Μεταβλητή είναι ένα γράμμα που παριστάνει οποιονδήποτε αριθμό. Η πιο γνωστή μεταβλητή είναι το x.
Μπορούμε να χρησιμοποιήσουμε και άλλα γράμματα, λατινικά (x, y, z, t, ...) και ελληνικά (α, β, γ, ...).
Και γιατί συμβαίνει αυτό;
Μα φυσικά, γιατί τα μαθηματικά αποτελούν μια παγκόσμια γλώσσα! Για να καταλάβετε τι σημαίνει αυτό επισκεφτείτε τον παρακάτω σύνδεσμο Τα μαθηματικά, μια παγκόσμια γλώσσα.
Παραστάσεις
Αριθμητική Παράσταση είναι μια παράσταση που περιέχει πράξεις και αριθμούς.
Αλγεβρική Παράσταση είναι μια παράσταση που περιλαμβάνει πράξεις, αριθμούς και μεταβλητές.
Για να το καταλάβετε, παρατηρήστε τον παρακάτω πίνακα:
| Αριθμητική Παράσταση | Αλγεβρική Παράσταση |
| Πράξεις | Πράξεις |
| Αριθμοί | Αριθμοί |
| Μεταβλητές | |
| Παραδείγματα | |
| 2•(5-4)+12:6 | 2(x-3)+4-2y |
Αριθμητικές Παραστάσεις έχουμε μάθει ήδη να λύνουμε. Ήρθε η ώρα να μάθουμε και τις αλγεβρικές!
Η αλγεβρικές παραστάσεις λύνονται με.... αναγωγή ομοίων όρων!
Αναγωγή ομοίων όρων είναι η διαδικασία με την οποία γράφουμε σε απλούστερη μορφή της αλγεβρικές παραστάσεις.
Είμαι σίγουρη ότι ακόμα δεν καταλάβατε τίποτα! Πάμε να δούμε τι σημαίνει ο ορισμός αυτός...
Σε αυτό το σημείο πρέπει να κάνουμε μια αναδρομή στο χρυσό κανόνα της πρόσθεσης και της αφαίρεσης.
Ας πούμε ότι έχω 2 λεμόνια και 3 πορτοκάλια... Τι έχω;
Αν έχω 5 καρέκλες και 1 αυτοκίνητο, τι έχω;
Αν έχω 4 τετράδια και 3 φράουλες, τι έχω;
Όπως καταλαβαίνετε, ο χρυσός κανόνας της πρόσθεσης και της αφαίρεσης είναι:
"Προσθέτουμε ή αφαιρούμε μόνο ίδια "πράγματα" και το αποτέλεσμα βγαίνει το ίδιο "πράγμα". Αυτό που αλλάζει είναι η ποσότητα."
Δηλαδή, όταν έχω 5 πορτοκάλια και φάω τα 3 πορτοκάλια, θα μείνουν 2 πορτοκάλια.
Και θα με ρωτήσετε τώρα, τι σχέση έχουν τα λεμόνια, τα πορτοκάλια και οι μεταβλητές...
Σε αυτό το επίπεδο, θα ήθελα να σκέφτεστε ότι μια μεταβλητή αντιπροσωπεύει ένα μοναδικό φρούτο. Για παράδειγμα το x είναι η φράουλα, το y είναι τα πορτοκάλια.
- 2x + 3x σημαίνει 2 φράουλες + 3 φράουλες.
Όμως, 2 φράουλες + 3 φράουλες = 5 φράουλες, οπότε
2x + 3x = 5x
- 8y - 6y σημαίνει 8 πορτοκάλια - 6 πορτοκάλια
Όμως, 8 πορτοκάλια - 6 πορτοκάλια = 2 πορτοκάλια, δηλαδή
8y - 6y = 2y
Πάμε να δούμε κάτι λίγο πιο δύσκολο.
2x +5y +7x -3y, σημαίνει έχουμε 2 φράουλες + 5 πορτοκάλια + 7 φράουλες - 3 πορτοκάλια.
Όμως, 2 φράουλες + 5 πορτοκάλια + 7 φράουλες - 3 πορτοκάλια = 9 φράουλες + 2 πορτοκάλια, δηλαδή
2x +5y +7x -3y = 9x+2y
Ο αριθμός που βρίσκεται αριστερά της μεταβλητής ονομάζεται συντελεστής.
- Όταν μια μεταβλητή δεν έχει συντελεστή, κρύβεται το 1. Δηλαδή,
x = 1x
Παρατήρηση: Στις αλγεβρικές παραστάσεις, συνήθως δε βάζουμε το σύμβολο του πολλαπλασιασμού μεταξύ αριθμών - μεταβλητών και μεταξύ μεταβλητών. Δηλαδή,
αντί για 2•x, γράφουμε 2x
αντί για x•y, γράφουμε xy.
Updated on October 17, 2024
1.4 Ευκλείδεια διαίρεση
Τώρα αρχίζουν τα δύσκολα... Διαίρεση... η πράξη που έχει δεχτεί τη μεγαλύτερη απόρριψη παγκοσμίως!
Και ο λόγος;
Γιατί είναι μια δύσκολη πράξη.
Αλήθεια, υπάρχουν δύσκολες πράξεις;
Πάμε να το ανακαλύψουμε μαζί!
Η διαίρεση είναι μια πολύ χρήσιμη πράξη, καθώς μας βοηθάει όταν:
- θέλουμε να χωρίσουμε, μοιράσουμε, διαιρέσουμε μια ποσότητα
- γνωρίζουμε τα πολλά και θέλουμε να βρούμε το ένα.
Οι διαίρεση σχετίζεται με 4 βασικούς αριθμούς:
- Διαιρετέος (Δ): η ποσότητα που θέλουμε τα μοιράσουμε
- διαιρέτης (δ): το πλήθος που θέλουμε να την μοιράσουμε
- πηλίκο (π): το αποτέλεσμά της
- υπόλοιπο (υ): το μέλος που μπορεί να μείνει.
Ας δούμε ένα παράδειγμα για να το καταλάβουμε.
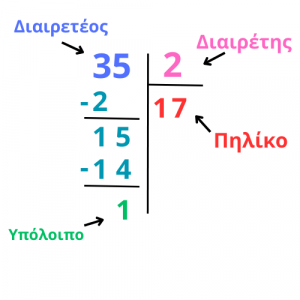
Και ποια είναι η σχέση που συνδέει αυτούς τους αριθμούς;
Παρατηρούμε ότι:
2•17+1=34+1=35
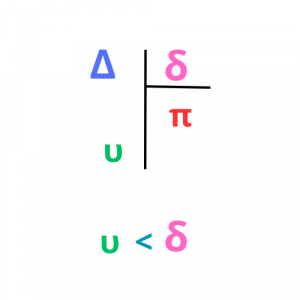
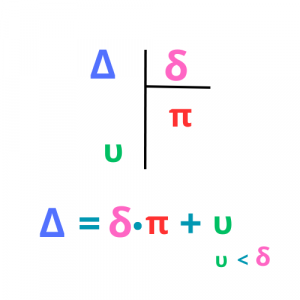
Προσοχή! Το υπόλοιπο πρέπει να είναι μικρότερο από το διαιρέτη.
Μια τέτοια διαίρεση ονομάζεται Ευκλείδεια Διαίρεση.
Η σχέση Δ=δ•π+υ ονομάζεται ταυτότητα της Ευκλείδειας Διαίρεσης.
Τέλεια διαίρεση ονομάζεται η διαίρεση, στην οποία το υπόλοιπο είναι 0.
Τότε η ταυτότητα της ευκλείδειας διαίρεσης γίνεται Δ=δ•π.
Η τέλεια διαίρεση είναι η αντίστροφη πράξη του πολλαπλασιασμού. Δηλαδή:
Δ=δ•π τότε Δ:δ=π ή Δ:π=δ
Αλγόριθμος της διαίρεσης
Πάμε να θυμηθούμε τη διαδικασία που μάθαμε στο δημοτικό:
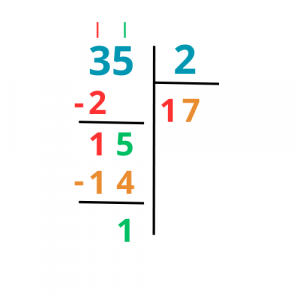
Να δούμε, όμως, και τον αλγόριθμο αλλιώς;
Και ποιος θα μας βοηθήσει εδώ;
Μα φυσικά η πρόσθεση!
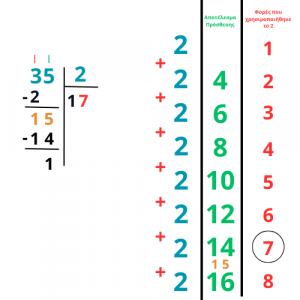
Τον αλγόριθμο μπορείτε να τον παρακολουθήσετε και στο σύνδεσμο Η διαίρεση αλλιώς.
Πηγή: Ευκλείδεια Διαίρεση , Κάθετη διαίρεση με μονοψήφιο διαιρέτη, ΚΑΘΕΤΗ ΔΙΑΙΡΕΣΗ , ΜΑΘΗΜΑΤΙΚΑ, teagher, Εκπαιδευτικό βίντεο από τo ΚΑΛΙΤΣΑ : https://mcjmcjmcj.wordpress.com/ , Άρθρο του μαθήματος:https://wp.me/PJcUD-8AP/
Ιδιότητες Διαίρεσης
- Ο διαιρέτης απαγορεύεται να είναι 0.
- Όταν Δ=δ, τότε π=1.
3:3=1
5:5=1
- Όταν δ=1, τότε π=Δ.
10:1=10
8:1=8
- Όταν Δ=0, τότε π=0.
0:5=0
0:100=0
Updated on October 13, 2024
1.2. Γωνία – Γραμμή – Επίπεδα σχήματα – Ευθύγραμμα σχήματα – Ίσα σχήματα
Πόσες φορές έχει τύχει να χτυπήσετε το πόδια σας στη γωνία κάποιου επίπλου... Αλήθεια ξέρετε τι είναι η γωνία;
Πάμε να ορίσουμε μαζί τη γωνία...
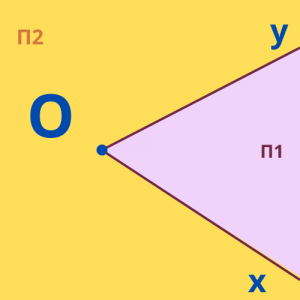
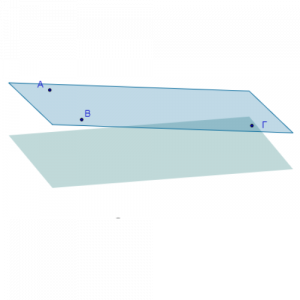
Αν σχεδιάσουμε δύο ημιευθείες Ox και Oy με κοινή αρχή το σημείο Ο, αυτές θα χωρίσουν το επίπεδο σε δύο περιοχές Π1 και Π2.
Κάθε μια από τις περιοχές αυτές μαζί με τις ημιευθείες Ox και Oy ονομάζεται γωνία.
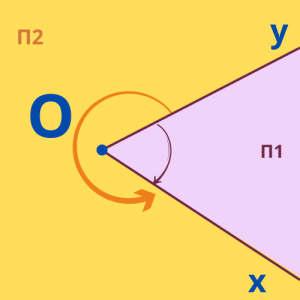
Η "μικρότερη" (Π1) λέγεται κυρτή
και η άλλη (Π2) μη κυρτή.
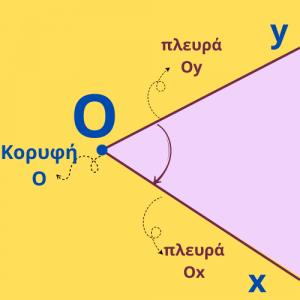
Το σημείο Ο ονομάζεται κορυφή τηςγωνίας και οι ημιευθείες Ox και Oy λέγονται πλευρές της γωνίας.
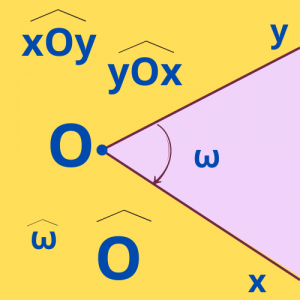
Ονομασία:
Τρίγωνο:
- Κορυφές Τριγώνου
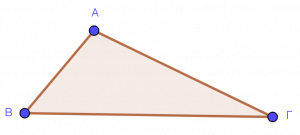
| Α |
| Β |
| Γ |
- Πλευρές τριγώνου
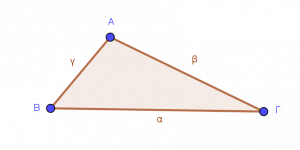
| ΑΒ | γ |
| ΑΓ | β |
| ΒΓ | α |
- Γωνίες τριγώνου
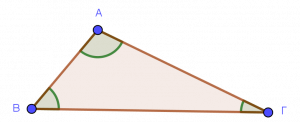
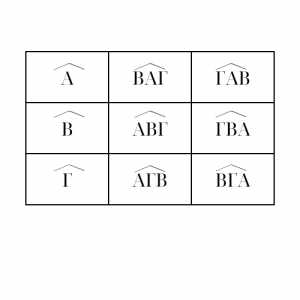
Περιεχόμενες γωνίες:
Δείτε τα παρακάτω σχήματα. Μπορείτε να καταλάβετε την έννοια της περιεχόμενης γωνίας;
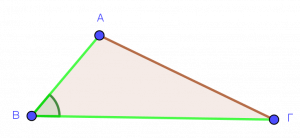
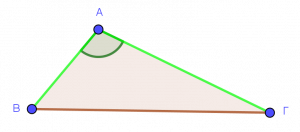
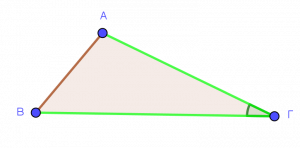
Περιεχόμενη ονομάζεται η γωνία που βρίσκεται ανάμεσα σε δύο πλευρές.
Προσκείμενες γωνίες:
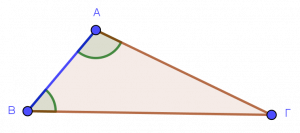
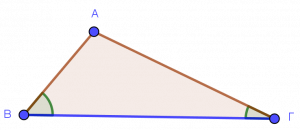
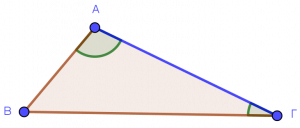
Προσκείμενες γωνίες ονομάζονται οι γωνίες του τριγώνου που έχουν μια κοινή πλευρά.
Απέναντι γωνίες ή απέναντι πλευρές:
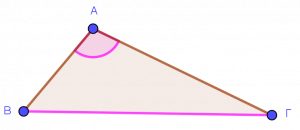
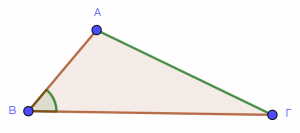
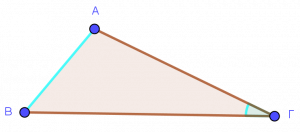
Στο πρώτο σχήμα λέμε η γωνία Α είναι απέναντι από την πλευρά ΒΓ, αλλά μπορούμε να πούμε ότι και η πλευρά ΒΓ είναι απέναντι από τη γωνία Α. Ομοίως και στα άλλα.
Για πάμε τώρα να δούμε αν τα καταλάβαμε όλα αυτά με ένα .... quizz!!!
https://create.kahoot.it/share/1-2/f2734867-c35c-46f5-bf7e-930b486870a3
Ευθύγραμμα Σχήματα
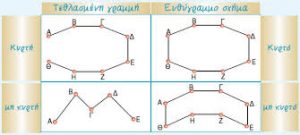Στο σχολικό βιβλίο υπάρχουν 4 νέες έννοιες που απεικονίζονται σε αυτή τη φωτογραφία. Αυτές είναι:
- τεθλασμένη γραμμή
- ευθύγραμμο σχήμα
- κυρτή τεθλασμένη γραμμή ή κυρτό ευθύγραμμο σχήμα
- μη κυρτή τεθλασμένη γραμμή ή μη κυρτό ευθύγραμμο σχήμα.
Πάμε να τα δούμε ένα ένα ξεχωριστά ( ή και μαζί).
Τεθλασμένη γραμμή - Ευθύγραμμο σχήμα
- Τεθλασμένη γραμμή είναι το σχήμα που που αποτελείται από διαδοχικά ευθύγραμμα τμήματα, τα οποία δε βρίσκονται όλα στην ίδια ευθεία.
- Ευθύγραμμο σχήμα ονομάζεται κάθε τεθλασμένη γραμμή, της οποίας τα άκρα συμπίπτουν.
Κυρτό - Μη κυρτό
Για να καταλάβετε την έννοια της κυρτότητας παρακολουθήστε το παρακάτω βίντεο:
Πηγή :Schoolnet, (2015 Απρίλιος 1) Α Γυμνασίου-Μαθηματικά-Γωνία, Γραμμή, Επίπεδα σχήματα, Ευθύγραμμα σχήματα, Ίσα σχήματα.
Εναλλακτικά μπορείτε να δείτε το βίντεο
Πηγή: Μανεάδης Γ., (2022, Δεκέμβριος 17) Κυρτή και μη κυρτή τεθλασμένη γραμμή.
Καταλήγουμε λοιπόν στο συμπέρασμα:
Μια τεθλασμένη γραμμή ονομάζεται κυρτή, όταν η προέκταση κάθε πλευράς της αφήνει όλες τις άλλες πλευρές στο ίδιο ημιεπίπεδο. Διαφορετικά λέγεται μη κυρτή.
Updated on October 12, 2024
1.1 Σημείο – Ευθύγραμμο τμήμα – Ευθεία – Ημιευθεία – Επίπεδο – Ημιεπίπεδο
Πάμε να ξεκινήσουμε με τις βασικές γεωμετρικές έννοιες. Σε αυτό το μάθημα θα θέσουμε τα θεμέλια της γεωμετρίας. Ο φίλος μας σε αυτό το ταξίδι θα είναι ο χάρακας.
Ο χάρακας λέγεται και κανόνας.
Ξεκινάμε λοιπόν...
Σημείο
Σημείο είναι μια κουκκίδα.
Συμβολισμός: Κεφαλαίο γράμμα π.χ. Α, Β κλπ
Ευθεία
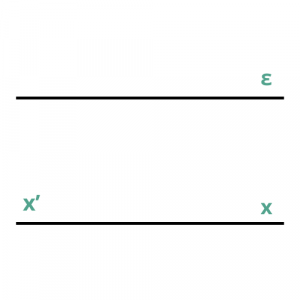Ευθεία είναι μια γραμμή που δεν έχει ούτε αρχή, ούτε τέλος.
Συμβολισμός:
- ένα μικρό γράμμα π.χ. ε, δ κλπ
- το ίδιο μικρό γράμμα, το οποίο επαναλαμβάνεται 2 φορές, από τις οποίες τη μια θα έχει τόνο. π.χ. χ'χ, y'y.
Ημιευθεία
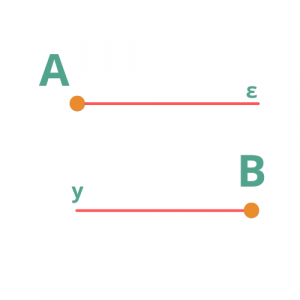Ημιευθεία είναι μια γραμμή που έχει αρχή αλλά δεν έχει τέλος.
Συμβολισμός:
κεφαλαίο και μικρό γράμμα π.χ. Αχ, By κλπ
Ευθύγραμμο τμήμα
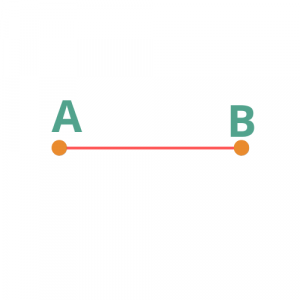Ευθύγραμμο τμήμα είναι μια γραμμή που έχει και αρχή και τέλος.
Συμβολισμός:
δύο κεφαλαία γράμματα ΑΒ ή ΒΑ
Αντικείμενες Ημιευθείες
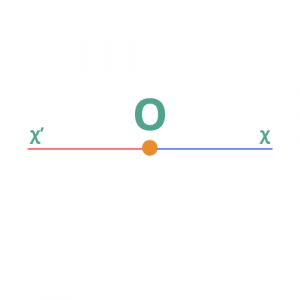Αντικείμενες ημιευθείες ονομάζονται δύο ευθείες που:
- έχουν κοινή αρχή
- μαζί σχηματίζουν μια ευθεία
Συμβολισμός:
Οχ και Οχ'
Παρατηρήσεις:
- Αν έχετε ένα σημείο, πόσες ευθείες μπορείτε να σχεδιάσετε που να διέρχονται από αυτό;
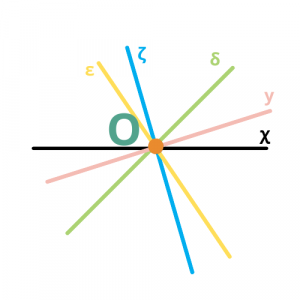Από ένα σημείο διέρχονται άπειρες ευθείες.
- Αν έχετε δύο σημεία, πόσες ευθείες μπορείτε να σχεδιάσετε, που να διέρχονται και από τα δύο;
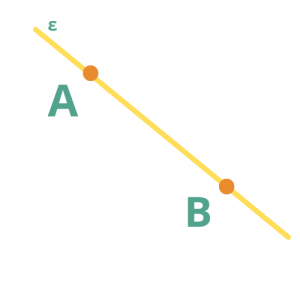
Από δύο σημεία διέρχεται μόνο μια ευθεία.
Προσοχή! Σε κάθε άσκηση, κάθε γράμμα μπορεί να χρησιμοποιηθεί ΜΟΝΟ μια φορά!
Επίπεδο
Το επίπεδο είναι μια δύσκολη έννοια να την κατανοήσουμε χωρίς οπτική επαφή. Για το λόγο αυτό θα μεταβούμε στη σελίδα Επίπεδο και ιδιότητες (του Χρήστου Γραμματικόπουλου) ώστε να εξερευνήσουμε μαζί όσα ακολουθούν στη θεωρία.
Επίπεδο είναι μια επιφάνεια, πάνω στην οποία εφαρμόζει παντού η ευθεία γραμμή.
- Ένα επίπεδο επεκτείνεται απεριόριστα.
- Από τρία μη συνευθειακά σημεία (είναι τα σημεία που δεν βρίσκονται στην ίδια ευθεία) διέρχεται ένα μοναδικό επίπεδο.
- Από ένα ή δύο σημεία διέρχονται άπειρα επίπεδα.
- Κάθε επίπεδο χωρίζει το χώρο σε δύο μέρη, ώστε, αν θέλουμε να περάσουμε από το ένα στο άλλο, πρέπει να διαπεράσουμε το επίπεδο.
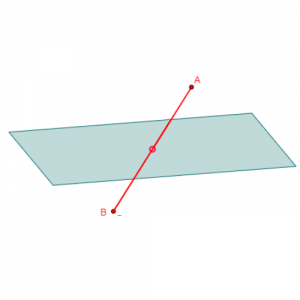
- Η ονομασία του επιπέδου είναι ένα κεφαλαίο γράμμα. π.χ. Π
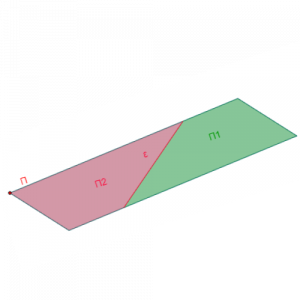
Ημιεπίπεδο
Κάθε ευθεία ενός επιπέδου το χωρίζει σε δύο μέρη που ονομάζονται ημιεπίπεδα.
Updated on November 17, 2024
Κεφάλαιο 1 – Βασικές Γεωμετρικές Έννοιες
Σας καλωσορίζω στον κόσμο της γεωμετρίας! Ένα κόσμο γεμάτο σχήματα, φαντασία, ομορφιά και δημιουργικότητα!!!!
Στο κεφάλαιο αυτό θα έρθουμε σε επαφή με βασικές γεωμετρικές έννοιες και θα μάθουμε πώς να σχεδιάζουμε τα βασικά γεωμετρικά σχήματα, καθώς και τις ιδιότητές τους.
Συγκεκριμένα θα ασχοληθούμε:
1.1 Σημείο – Ευθύγραμμο τμήμα – Ευθεία – Ημιευθεία – Επίπεδο – Ημιεπίπεδο
1.1 Σημείο – Ευθύγραμμο τμήμα – Ευθεία – Ημιευθεία – Επίπεδο – Ημιεπίπεδο
1.2 Γωνία – Γραμμή – Επίπεδα σχήματα – Ευθύγραμμα σχήματα – Ίσα σχήματα
1.2. Γωνία – Γραμμή – Επίπεδα σχήματα – Ευθύγραμμα σχήματα – Ίσα σχήματα
1.3 Μέτρηση, σύγκριση και ισότητα ευθυγράμμων τμημάτων – Απόσταση σημείων – Μέσο ευθυγράμμου τμήματος
1.4 Πρόσθεση και αφαίρεση ευθυγράμμων τμημάτων
1.5 Μέτρηση, σύγκριση και ισότητα γωνιών – Διχοτόμος γωνίας
1.6 Είδη γωνιών – Κάθετες ευθείες
1.7 Εφεξής και διαδοχικές γωνίες – Άθροισμα γωνιών
1.8 Παραπληρωματικές και Συμπληρωματικές γωνίες – Κατακορυφήν γωνίες
1.9 Θέσεις ευθειών στο επίπεδο
1.10 Απόσταση σημείου από ευθεία – Απόσταση παραλλήλων
1.11 Κύκλος και στοιχεία του κύκλου
1.12 Επίκεντρη γωνία
1.13 Θέσεις ευθείας και κύκλου
Updated on October 6, 2024
Δυνάμεις Φυσικών Αριθμών – Προτεραιότητα Πράξεων
Για πάμε να εξερευνήσουμε τις δυνάμεις... Σας θυμίζει κάτι το 23;
Τις δυνάμεις τις έχουμε συναντήσει στο Δημοτικό. Πάμε να θυμηθούμε, όμως, τι είναι οι δυνάμεις και τι γνωρίζουμε για αυτές. Ας δούμε πρώτα ένα παράδειγμα.
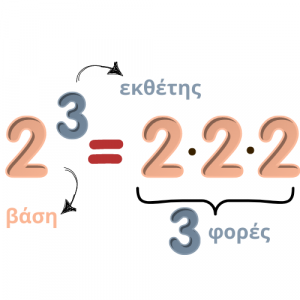
Δύναμη
Η γενική της μορφή είναι :
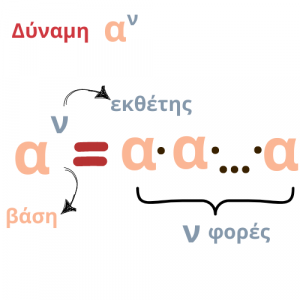
Ονομασία:
- Η δύναμη αν διαβάζεται νιοστή δύναμη του α ή α στη ν.
- Η δύναμη α2 διαβάζεται α στη δευτέρα ή α στο τετράγωνο ή τετράγωνο του α.
- Η δύναμη α3 διαβάζεται α στην τρίτη ή α στον κύβο ή κύβος του α.
Συχνό Λάθος:
Εδώ χρειάζεται ιδιαίτερη προσοχή, ώστε να μην υπολογίζετε τη δύναμη ως πολλαπλασιασμό της βάσης και του εκθέτη. Δηλαδή:
23=2•3=6 Αυτό είναι ΛΑΘΟΣ!!!! Το σωστό είναι: 23=2•2•2=8.
Ιδιότητες Ορισμού:
- α1=α
- 1ν=1
- 00 δεν ορίζεται
- 0ν=0
Προτεραιότητα Πράξεων
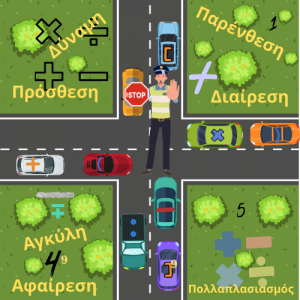
Εμείς έχουμε συνηθίσει να κάνουμε κάθε πράξη ξεχωριστά. Τι γίνεται, όμως, αν μας δοθούν πολλές πράξεις μαζί; Ποια θα κάναμε πρώτα; Ας πούμε, για παράδειγμα, ότι μας δίνεται:
2•(10-8)+25:5-3+16
Ας τα πάρουμε τα πράγματα από την αρχή! Το παράδειγμα που μας δόθηκε αποτελεί μια αριθμητική παράσταση.
Αριθμητική Παράσταση ονομάζεται κάθε σειρά αριθμών που συνδέονται μεταξύ τους με τα σύμβολα των πράξεων.
Στις αριθμητικές παραστάσεις δεν επιλέγουμε εμείς τη σειρά που θα γίνουν οι πράξεις, αλλά υπάρχει "κάποιος" που ρυθμίζει τη σειρά αυτή.
Αυτός ο "κάποιος" είναι η προτεραιότητα πράξεων.
Η Προτεραιότητα Πράξεων αναφέρεται στη σειρά με την οποία γίνονται οι πράξεις σε μια αριθμητική παράσταση και είναι η ακόλουθη:
Για πάμε να λύσουμε την παραπάνω παράσταση...
2•(10-8)+25:5-3+16=
2•(10-8)+25:5-3+16=
2•2+25:5-3+16=
2•2+25:5-3+1=
4+5-3+1=
9-3+1=
6+1= 7
Μπορείτε να σημειώσετε κάποιες παρατηρήσεις σχετικά με το προηγούμενο παράδειγμα; Προσέξτε τι γίνεται με τους αριθμούς και τις πράξεις που δε χρησιμοποιούμε, καθώς και όταν έχουμε πράξεις που βρίσκονται στο ίδιο βήμα.
Είμαι σίγουρη ότι ακόμα και τώρα είναι αρκετές οι απορίες σχετικά με την προτεραιότητα πράξεων. Στον παρακάτω σύνδεσμο θα σας λυθούν όλες οι απορίες, καθώς περιλαμβάνει παρατηρήσεις, αναλυτικό παράδειγμα, καθώς και ασκήσεις για εμπέδωση και αφομοίωση της νέας γνώσης.
Tip! Μέχρι να εξοικειωθείτε με την προτεραιότητα των πράξεων, θα σας βοηθήσει πολύ να χρησιμοποιείτε:
- χρώματα, με τα οποία θα υπογραμμίζετε την πράξη ή τις πράξεις που πρέπει να γίνουν στο βήμα που είστε και
- χάρακα, ώστε να κρύβετε τα προηγούμενα βήματα.
Επίσης, τις αριθμητικές παραστάσεις να τις κάνετε πάντα κάθετα και όχι οριζόντια. Βοηθάει πολύ!
Updated on October 2, 2024
Δυνάμεις Ρητών Αριθμών με εκθέτη ακέραιο
Στην προηγούμενη ενότητα είδαμε ότι για να διαιρέσουμε δυνάμεις με την ίδια βάση, αφήνουμε την ίδια βάση και βάζουμε ως εκθέτη τη διαφορά των εκθετών. Δηλαδή:
78:76=78-6=72=49
Θα μπορούσαμε, όμως, να έχουμε:
76:78=76-8=7-2
Δε χρειάζεται πανικός! Πάμε να σκεφτούμε λογικά, όπως πάντα! Παρατηρήστε τις παρακάτω εικόνες:
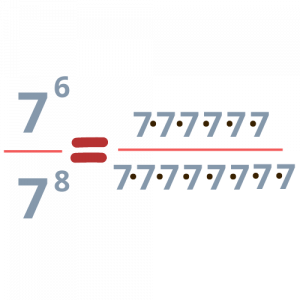
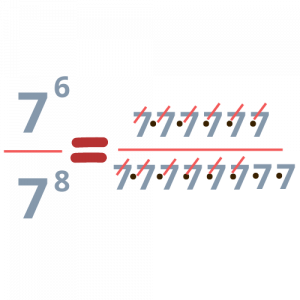
Άρα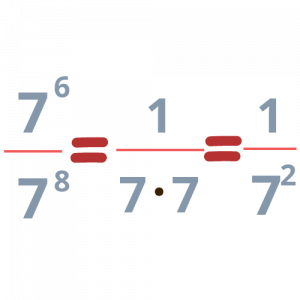
Όμως, από τις ιδιότητες δυνάμεων ισχύει: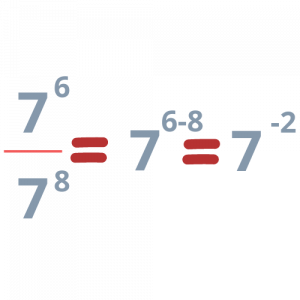
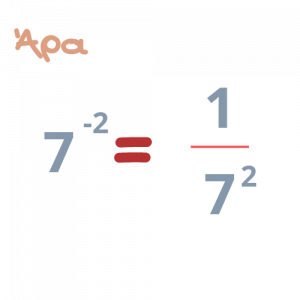
Συνεπώς, η δύναμη κάθε αριθμού, διάφορου του μηδενός, με εκθέτη αρνητικό είναι ίση με κλάσμα που έχει αριθμητή τη μονάδα και παρονομαστή τη δύναμη του αριθμού αυτού με αντίθετο εκθέτη.
Δηλαδή ισχύει:
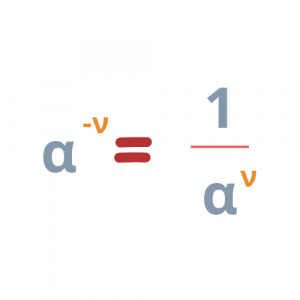
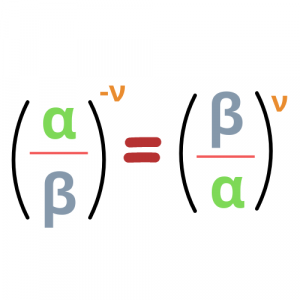
- Οι ιδιότητες των δυνάμεων με εκθέτη φυσικό ισχύουν και για τις δυνάμεις με εκθέτη ακέραιο.
Προσοχή!!!! Το αρνητικό πρόσημο του εκθέτη, δε σχετίζεται με το πρόσημο της βάσης!
Δηλαδή, (-2)-3=(-1/2)3.
Αυτό σημαίνει ότι το - στον εκθέτη σχετίζεται μόνο με την αντιστροφή του κλάσματος. Αφού αντιστρέψουμε το κλάσμα, τότε ανάλογα με τον εκθέτη που έχουμε, υπολογίζουμε το πρόσημο της βάσης.
Δυνάμεις Ρητών με εκθέτη ακέραιο
Updated on October 1, 2024
Δυνάμεις Ρητών Αριθμών με εκθέτη φυσικό
Για πάμε να εξερευνήσουμε ένα δύσκολο κομμάτι των μαθηματικών... Σας θυμίζει κάτι το 23;
Τις δυνάμεις τις έχουμε συναντήσει στο Δημοτικό και στην αρχή της Α' Γυμνασίου. Πάμε να θυμηθούμε, όμως, τι είναι οι δυνάμεις και τι γνωρίζουμε για αυτές. Ας δούμε πρώτα ένα παράδειγμα.
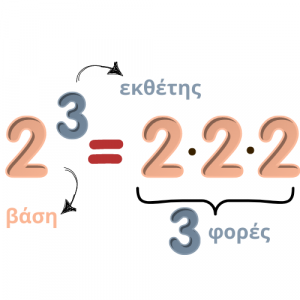
Δύναμη
Η γενική της μορφή είναι :
Υπενθύμιση:
- Η δύναμη αν διαβάζεται νιοστή δύναμη του α ή α στη ν.
- Η δύναμη α2 διαβάζεται α στη δευτέρα ή α στο τετράγωνο ή τετράγωνο του α.
- Η δύναμη α3 διαβάζεται α στην τρίτη ή α στον κύβο ή κύβος του α.
Συχνό Λάθος:
Εδώ χρειάζεται ιδιαίτερη προσοχή, ώστε να μην υπολογίζετε τη δύναμη ως πολλαπλασιασμό. Δηλαδή:
23=2•3=6 Αυτό είναι ΛΑΘΟΣ!!!! Το σωστό είναι: 23=2•2•2=8.
Ιδιότητες Ορισμού:
- α1=α
- 1ν=1
- 00 δεν ορίζεται
- α0=1 , όπου α≠0
Πρόσημο Δύναμης
Καλό το 23 αλλά τι γίνεται με το -23;
και όχι μόνο αυτό... Αλήθεια, τι θα κάνατε σε καθεμία από τις παρακάτω περιπτώσεις;
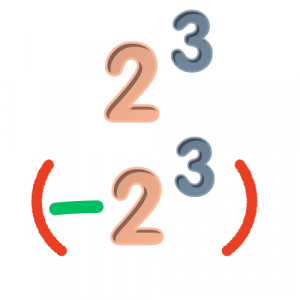
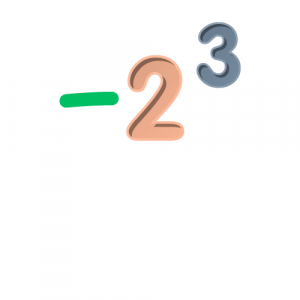
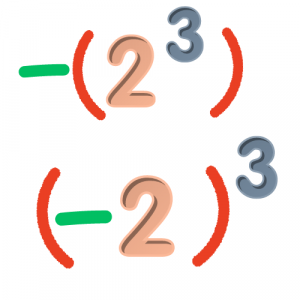
Ο γενικός κανόνας υπολογισμού των δυνάμεων είναι ίδιος και στην περίπτωση που έχουμε πρόσημα. Αυτό που πρέπει να ξεχωρίσετε σε πρώτη φάση είναι πότε ο εκθέτης επηρεάζει το πρόσημο και πότε όχι, με άλλα λόγια ποια είναι η βάση της δύναμης.
εδώ η βάση της δύναμης είναι το 2, οπότε ο εκθέτης επηρεάζει μόνο το 2 και όχι το -.
εδώ η βάση της δύναμης είναι το 2, οπότε ο εκθέτης επηρεάζει μόνο το 2 και όχι το -.
εδώ η βάση της δύναμης είναι το -2, οπότε ο εκθέτης επηρεάζει και το πρόσημο και το 2.
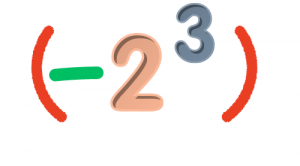
εδώ η βάση της δύναμης είναι το 2, οπότε ο εκθέτης επηρεάζει μόνο το 2 και όχι το -.
- Όταν η βάση είναι θετικός αριθμός υπολογίζουμε τις δυνάμεις, όπως ήδη ξέρουμε, και το αποτέλεσμα βγαίνει πάντα θετικός αριθμός. Τι γίνεται, όμως, όταν η βάση είναι αρνητικός αριθμός;
Παρατηρείστε καλά τις παρακάτω φωτογραφίες και προσπαθήστε να καταλήξετε σε κάποιο συμπέρασμα.
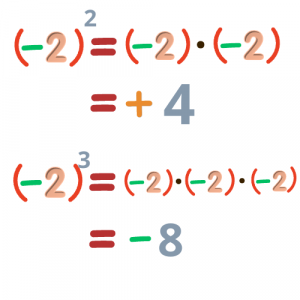
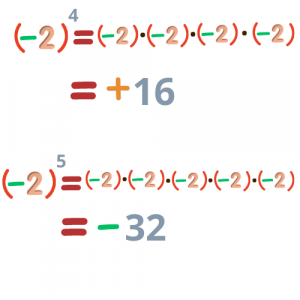
Παρατηρούμε ότι όταν η βάση είναι αρνητικός αριθμός, το αποτέλεσμα δεν είναι πάντα αρνητικό. Μπορείτε να καταλάβετε πότε είναι θετικός και πότε αρνητικός αριθμός το αποτέλεσμα;
Το πρόσημο εξαρτάται από τον εκθέτη και συγκεκριμένα:
- όταν ο εκθέτης είναι άρτιος / ζυγός αριθμός (2, 4, 6,...) το αποτέλεσμα βγαίνει θετικός αριθμός
- όταν ο εκθέτης είναι περιττός / μονός αριθμός (1, 3, 5,...) το αποτέλεσμα βγαίνει αρνητικός αριθμός.
Δυνάμεις Ρητών με εκθέτη φυσικό αριθμό
Ιδιότητες Πράξεων
| Ίδια βάση | Κανόνας | Παράδειγμα |
| Πολλαπλασιασμός | αν•αμ=αν+μ | 23•25=23+5=28 |
| Διαίρεση | αν:αμ=αν-μ | 35:32=35-2=33 |
| αν/αμ=αν-μ | 35/32=35-2=33 | |
| Ίδιος εκθέτης | ||
| Πολλαπλασιασμός | αν•βν=(α•β)ν | 23•53=(2•5)3=103 |
| Διαίρεση | αν:βν=(α:β)ν | 103:53=(10:5)3=23 |
| αν/βν=(α/β)ν | 103/53=(10/5)3=23 | |
| Δύναμη σε δύναμη | (αν)μ=αν•μ | (23)4=23•4=212 |
Παρατηρήσεις:
- Οι ιδιότητες δυνάμεων ισχύουν μόνο στις πράξεις του πολλαπλασιασμού και της διαίρεσης. Στην πρόσθεση και στην αφαίρεση ακολουθούμε την προτεραιότητα των πράξεων, όπως στο παράδειγμα 23+24=8+16=24.
- Αυτό που είναι ίδιο (βάση ή εκθέτης) μένει ίδιο.
- Οι ιδιότητες δυνάμεων ισχύουν και αντίστροφα.
- Προσπαθήστε να ξεχωρίσετε την πρώτη και την τελευταία ιδιότητα!
Ασκήσεις στις Δυνάμεις με εκθέτη φυσικό αριθμό
Updated on September 30, 2024
Δεκαδική Μορφή Ρητών Αριθμών
Ήρθε η ώρα να κάνουμε μια μικρή αναφορά στους δεκαδικούς αριθμούς.
Ίσως οι δεκαδικοί αριθμοί να μην είναι οι αγαπημένοι μας, γιατί και αυτοί έχουν τους δικούς τους κανόνες. Ωστόσο, πρέπει να γνωρίζουμε ότι οι δεκαδικοί αριθμοί είναι και αυτοί αριθμοί και μπορεί να έχουν πρόσημα. Οι κανόνες των προσήμων συνδυάζονται με τους κανόνες των δεκαδικών.
Εδώ, όμως, δε θα ασχοληθούμε με αυτά, αλλά με μια ειδική περίπτωση των δεκαδικών αριθμών που ονομάζονται περιοδικοί αριθμοί.
Περιοδικοί Αριθμοί
Για να ρίξουμε μια ματιά στην παρακάτω εικόνα... Παρατηρείτε κάτι;
Για ρίξτε άλλη μια ματιά...
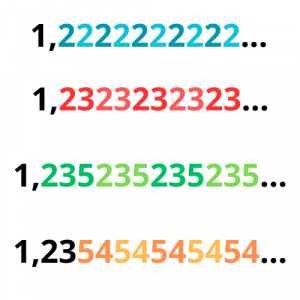
Νομίζω τώρα φαίνεται ξεκάθαρα ότι πρόκειται για δεκαδικούς αριθμούς με άπειρο πλήθος δεκαδικών, στους οποίους κάποια ψηφία επαναλαμβάνονται.
Περιοδικοί αριθμοί ονομάζονται οι δεκαδικοί αριθμοί με άπειρα δεκαδικά ψηφία, στους οποίους κάποια ψηφία επαναλαμβάνονται διαρκώς.
Το τμήμα των επαναλαμβανόμενων δεκαδικών ψηφίων κάθε περιοδικού αριθμού ονομάζεται περίοδος.
Συμβολισμός:
Κάθε ρητός αριθμός μπορεί να έχει τη μορφή δεκαδικού αριθμού ή περιοδικού αριθμού και αντίστροφα.
Και πώς μπορεί ένας ρητός να γίνει δεκαδικός;
Εδώ πρέπει να θυμηθούμε ποια πράξη κρύβεται στα κλάσματα... Μα φυσικά η διαίρεση!
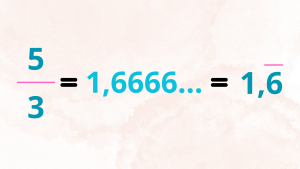
Και πώς μπορεί ένας δεκαδικός να γίνει ρητός;
Εδώ η διαδικασία είναι λίγο πιο δύσκολη. Πάμε να κάνουμε ένα παράδειγμα για να το καταλάβουμε.
Σε αυτό το σημείο μπορείτε να ασχοληθείτε με τις ασκήσεις 1, 2, 3 του σχολικού βιβλίου, που βρίσκονται στη σελίδα 136.