Updated on September 24, 2024
Διαίρεση Ρητών
 Σε αυτό το σημείο έχω να σας πω ένα πολύ ευχάριστο νέο...η διαίρεση ακολουθεί τους ίδιους κανόνες προσήμων με τον πολλαπλασιασμό.
Σε αυτό το σημείο έχω να σας πω ένα πολύ ευχάριστο νέο...η διαίρεση ακολουθεί τους ίδιους κανόνες προσήμων με τον πολλαπλασιασμό.

Για πάμε να δούμε, όμως, αν τους θυμόμαστε...
Προσοχή εδώ! Κάνουμε διαίρεση.

Άσκηση Αυτοαξιολόγησης στη Διαίρεση Ρητών
Ωστόσο, επειδή τη διαίρεση μπορούμε να τη δούμε και με τη μορφή κλάσματος, είναι καλό σε αυτό το σημείο να μιλήσουμε για το πρόσημο του κλάσματος.
Πρόσημο σε ένα κλάσμα μπορούμε να έχουμε:
- αριστερά από το κλάσμα
- στον αριθμητή
- στον παρονομαστή
Για να καταλάβετε τι λέμε, παρατηρείστε τα παρακάτω παραδείγματα.
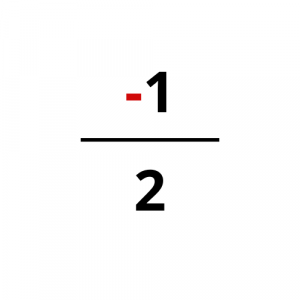
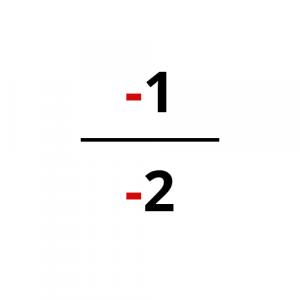
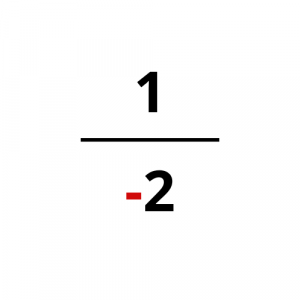
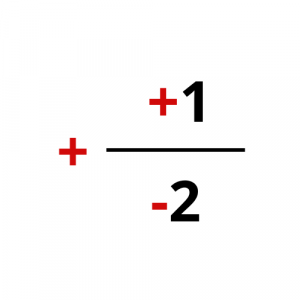
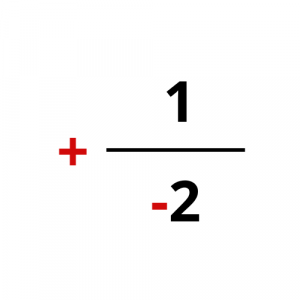
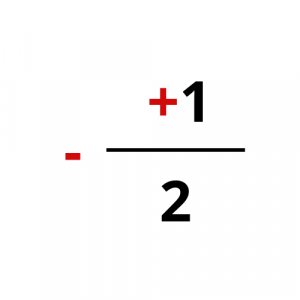
Ωστόσο, το πρόσημο του κλάσματος πρέπει να είναι ένα και να βρίσκεται στα αριστερά του (μπροστά από την κλασματική γραμμή).
Για να υπολογίσουμε το πρόσημο του κλάσματος ακολουθούμε τον κανόνα των προσήμων στο γινόμενο πολλών παραγόντων.
Σε αυτό το σημείο μπορείτε να προσπαθήσετε να υπολογίσετε το πρόσημο των παραπάνω κλασμάτων και να συγκρίνετε τις απαντήσεις σας με τις εικόνες που ακολουθούν.
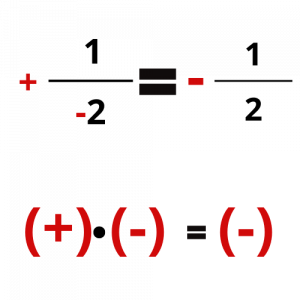
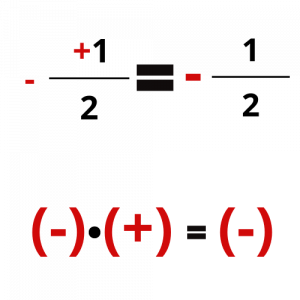
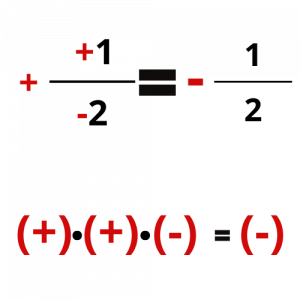
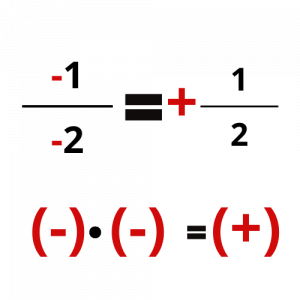
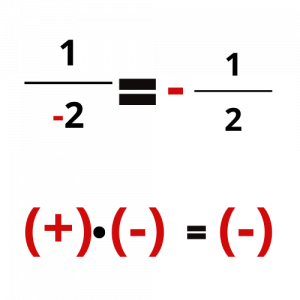
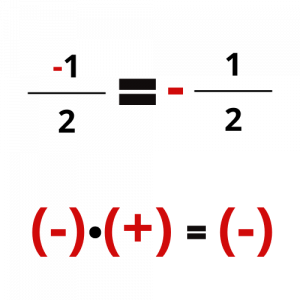
Τι λέτε... είστε έτοιμοι για ένα κουίζ???

Δραστηριότητα Αυτοαξιολόγησης στο Πρόσημο Κλασμάτων
Για πάμε να κάνουμε λίγο παραπάνω εξάσκηση...
 Το παρακάτω φύλλο εργασιών περιλαμβάνει ασκήσεις πάνω στη διαίρεση, καθώς και μια συνδυαστική άσκηση, η οποία περιλαμβάνει όλες τις πράξεις.
Το παρακάτω φύλλο εργασιών περιλαμβάνει ασκήσεις πάνω στη διαίρεση, καθώς και μια συνδυαστική άσκηση, η οποία περιλαμβάνει όλες τις πράξεις.
Updated on September 28, 2024
Πολλαπλασιασμός Ρητών

Και αν τώρα νοιώθετε λίγο ανακουφισμένοι, ετοιμαστείτε να μπερδευτούμε ξανά...! Και αν αναρωτιέστε γιατί να συμβαίνει αυτό... η απάντηση είναι ... μα φυσικά γιατί ο πολλαπλασιασμός έχει διαφορετικούς κανόνες από την πρόσθεση και την αφαίρεση....

Θα το ξεπεράσουμε, όμως, μαζί και αυτό! Θυμηθείτε το παν στα μαθηματικά είναι η καλή διάθεση και η εξάσκηση!
Πάμε να ξεκινήσουμε και αυτό το ταξίδι με ένα παραμύθι...
Κόκκινη κλωστή δεμένη, στην ανέμη τυλιγμένη, δώσ' της κλώτσο να γυρίσει, παραμύθι ν' αρχινίσει.
Η παραπάνω ιστορία προσπαθεί να μας εξηγήσει τους κανόνες προσήμων που ισχύουν στον πολλαπλασιασμό, οι οποίες συνοψίζονται στην παρακάτω φωτογραφία.

Προσέξτε εδώ τη δύναμη που έχει το -. Όμως, η ένωση δύο - κάνουν ένα +!
Το ευχάριστο με τον πολλαπλασιασμό είναι ότι πρέπει να προσέξουμε μόνο το πρόσημο που θα επιλέξουμε και όχι την πράξη, καθώς κάνουμε πάντα πολλαπλασιασμό!
Αλήθεια παρατηρείτε κάτι περίεργο στη φωτογραφία; Για να σας βοηθήσω... γιατί υπάρχουν οι παρενθέσεις;

Σας υπενθυμίζω ότι τα σύμβολά των πράξεων είναι τσακωμένα μεταξύ τους, γι' αυτό δε θα τα δείτε ποτέ το ένα δίπλα στο άλλο. Το ρόλο του διαιτητή παίζει πάντα η παρένθεση!
Για να δούμε τώρα αν έχουμε καταλάβει πώς λειτουργεί ο πολλαπλασιασμός... Είστε έτοιμοι για ένα παιχνιδάκι?

Ο παρακάτω σύνδεσμος αποτελεί μια άσκηση αυτοαξιολόγησης πάνω στον πολλαπλασιασμό των ρητών με τη μορφή quiz. Καλή επιτυχία!
Άσκηση Αυτοαξιολόγησης στον Πολλαπλασιασμό
Ιδιότητες πολλαπλασιασμού
Οι ιδιότητες του πολλαπλασιασμού παραμένουν ίδιες. Συγκεκριμένα :
- Αντιμεταθετική ιδιότητα
α · β = β · α
- Προσεταιριστική Ιδιότητα
α · (β · γ)=(α · β) · γ
- Επιμεριστική Ιδιότητα
α · (β + γ) = α · β + α · γ
α · (β - γ) = α · β - α · γ
- Ουδέτερο στοιχείο είναι το 1.
α · 1 = 1 · α = 1
- Το γινόμενο ρητού με το 0 ισούται με 0.
0 · α = α · 0 = 0
Γινόμενο Πολλών Παραγόντων
- Αν ένας τουλάχιστον παράγοντας είναι 0, τότε και το γινόμενο είναι ίσο με 0.
- Αν όλοι οι παράγοντες είναι θετικοί, τότε το γινόμενο είναι θετικό.
- Αν υπάρχουν θετικοί και αρνητικοί παράγοντες, τότε πολλαπλασιάζουμε τις απόλυτες τιμές τους και βάζουμε:
-
- Το πρόσημο +, αν το πλήθος των αρνητικών παραγόντων είναι άρτιο / ζυγό.
- Το πρόσημο -, αν το πλήθος των αρνητικών παραγόντων είναι περιττό / μονό.
-
Για πάμε να δούμε αν τα έχουμε εμπεδώσει όλα αυτά...
 Το παρακάτω φύλλο εργασιών περιλαμβάνει ασκήσεις στον πολλαπλασιασμό ρητών, καθώς και μια συνδυαστική άσκηση με την πρόσθεση και την αφαίρεση ρητών.
Το παρακάτω φύλλο εργασιών περιλαμβάνει ασκήσεις στον πολλαπλασιασμό ρητών, καθώς και μια συνδυαστική άσκηση με την πρόσθεση και την αφαίρεση ρητών.
Updated on September 27, 2024
1.1. Φυσικοί Αριθμοί – Διάταξη – Στρογγυλοποίηση
Οι φυσικοί αριθμοί (ή αριθμοί της φύσης για τους ρομαντικούς) είναι οι αριθμοί 0, 1, 2, 3, 4, 5, ..., 10000, 10001, ...
Βασική ιδιότητα: Κάθε αριθμός έχει έναν προηγούμενο και έναν επόμενο αριθμό.
Κατηγορίες:
Άρτιοι ή Ζυγοί είναι οι φυσικοί αριθμοί που διαιρούνται με το 2.
π.χ. 2, 4, 6,...
Περιττοί ή Μονοί είναι οι φυσικοί αριθμοί που ΔΕΝ διαιρούνται με το 2.
π.χ. 1, 3, 5, ...
Δεκαδικό Σύστημα Αρίθμησης
Γνωρίζετε ότι μπορούμε να φτιάξουμε άπειρους αριθμούς, χρησιμοποιώντας μόνο 10 ψηφία;
Και όμως! Όλοι οι αριθμοί δημιουργούνται χρησιμοποιώντας τα ψηφία 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
- Η αξία κάθε ψηφίου καθορίζεται από τη θέση που κατέχει.
Παρατηρήστε την παρακάτω φωτογραφία.
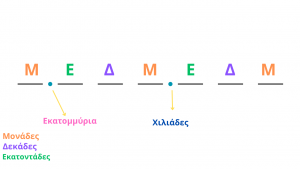
Το μοτίβο μονάδες, δεκάδες, εκατοντάδες επαναλαμβάνεται στις τάξεις των ψηφίων. Ωστόσο, μόνο την πρώτη φορά γράφονται σκέτα. Τα υπόλοιπα συνοδεύονται από τις χιλιάδες, εκατομμύρια, δισεκατομμύρια κλπ.
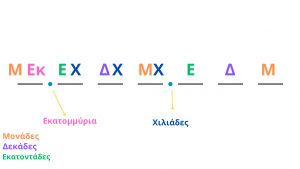
Στρογγυλοποίηση
Η στρογγυλοποίηση είναι μια έννοια που έχετε ασχοληθεί στο δημοτικό. Αλλά εμείς θα τη δούμε πάλι από την αρχή! Για πάμε να θυμηθούμε τους κανόνες μαζί!
Στην παρακάτω παρουσίαση περιγράφεται η έννοια της στρογγυλοποίησης, οι κανόνες, καθώς και παραδείγματα για εμπέδωση.
Updated on Oktober 29, 2024
Κεφάλαιο 1 – Φυσικοί Αριθμοί
Καλώς ήρθατε στον κόσμο των Φυσικών Αριθμών. Ο κόσμος αυτός είναι ιδιαίτερα γνώριμος για εσάς, καθώς τον γνωρίσατε και τον εξερευνήσατε στο Δημοτικό. Πάμε να κάνουμε ένα γρήγορο πέρασμα στα παλιά μας λημέρια και να αναπολήσουμε όμορφες στιγμές με τους φίλους μας τους αριθμούς, τς πράξεις, τη στρογγυλοποίηση, το ΕΚΠ, το ΜΚΔ κλπ.
Τα αναμενόμενα μαθησιακά αποτελέσματα από τη μελέτη της ενότητας αυτής είναι να:
- μπορείτε να κάνετε τις 4 πράξεις σωστά
- στρογγυλοποιείτε αριθμούς
- εφαρμόζετε την προτεραιότητα των πράξεων
- αναγνωρίζετε τα κριτήρια διαιρετότητας
- βρίσκετε το ΕΚΠ και το ΜΚΔ αριθμών.
Καλή σας διασκέδαση!
1.1. Φυσικοί Αριθμοί - Διάταξη Φυσικών - Στρογγυλοποίηση
1.1. Φυσικοί Αριθμοί – Διάταξη – Στρογγυλοποίηση
1.2. Πρόσθεση, Αφαίρεση και Πολλαπλασιασμός Φυσικών Αριθμών
1.3. Δυνάμεις Φυσικών Αριθμών
Δυνάμεις Φυσικών Αριθμών – Προτεραιότητα Πράξεων
1.4. Ευκλείδεια Διαίρεση - Διαιρετότητα
1.5. Χαρακτήρες Διαιρετότητας - ΜΚΔ - ΕΚΠ - Ανάλυση Αριθμού σε γινόμενο πρώτων παραγόντων
Α.1.5. Χαρακτήρες Διαιρετότητας – ΜΚΔ – ΕΚΠ – Ανάλυση Αριθμού σε γινόμενο πρώτων παραγόντων
Updated on September 24, 2024
Αφαίρεση Ρητών

Η αφαίρεση των ρητών βασίζεται στην πρόσθεση, καθώς όπως έχουμε αναφέρει, δεν καθορίζει το σύμβολο της πράξης την πράξη που θα κάνουμε, αλλά τα πρόσημα!
Υπάρχουν δύο τεχνικές που μπορούμε να ακολουθήσουμε στην αφαίρεση ρητών.

Προσθέτουμε στον Μειωτέο των αντίθετο του Αφαιρετέου.
π.χ.
- 2 - (+ 4) = - 2 + (- 4)= - 6
- 10 - (- 3) = - 10 + (+3) = - 7
Το παρακάτω φύλλο εργασιών περιλαμβάνει ασκήσεις για εξάσκηση πάνω στην απαλοιφή παρενθέσεων. Για πάμε...
Κάνουμε απαλοιφή παρενθέσεων.
Τι είναι η Απαλοιφή Παρενθέσεων;

Απαλοιφή παρενθέσεων σημαίνει ότι διώχνουμε τις παρενθέσεις και τα σύμβολα των πράξεων, ώστε να έχουμε μόνο αριθμούς και πρόσημα και α ακολουθούμε τους κανόνες τις πρόσθεσης.
- όταν μπροστά από την παρένθεση δεν υπάρχει τίποτα ή υπάρχει το +, τότε φεύγει η παρένθεση μαζί με το + που βρίσκεται μπροστά της (αν υπάρχει) και αντιγράφουμε ό,τι υπάρχει μέσα στην παρένθεση.
π.χ.
+ (-2) = - 2
+ (+4) + (-2) = +4 -2
- όταν μπροστά από την παρένθεση υπάρχει -, τότε φεύγει η παρένθεση μαζί με το - που βρίσκεται μπροστά της και αντιγράφουμε ό,τι βρίσκεται μέσα στην παρένθεση με αλλαγμένα πρόσημα.
π.χ.
- (+4) = - 4
- (-8) - (-2) - (+3) = +8 +2 -3
και βέβαια, στις παραστάσεις, συνεχίζουμε τις πράξεις, ακολουθώντας τους κανόνες της πρόσθεσης.
Πάμε να δούμε αν μπορούμε να εφαρμόσουμε αυτά που μάθαμε στην πράξη...

Το παρακάτω φύλλο εργασιών περιλαμβάνει ασκήσεις για εξάσκηση πάνω στην απαλοιφή παρενθέσεων. Για πάμε...
Πριν προχωρήσετε στις παρακάτω ενότητες, βεβαιωθείτε ότι έχετε κατανοήσει πλήρως την πρόσθεση και την αφαίρεση ρητών αριθμών, καθώς ο πολλαπλασιασμός και η διαίρεση έχουν άλλους κανόνες! Γι' αυτό θα ήταν καλό σε αυτό το σημείο να κάνετε μια μικρή επανάληψη!

Προκειμένου να αξιολογήσετε το βαθμό που έχετε κατανοήσει αυτές της έννοιες, μπορείτε να κάνετε την παρακάτω Δραστηριότητα Αυτοαξιολόγησης.
Updated on September 24, 2024
Πρόσθεση Ρητών

Τώρα αρχίζουν τα δύσκολα... Στο Δημοτικό είχαμε μάθει ότι το + είναι το σύμβολο της πρόσθεσης και το - είναι το σύμβολο της αφαίρεσης. Όμως, το + και το - εκτός από σύμβολα πράξεων είναι και πρόσημα... Πώς θα μπορέσω να τα ξεχωρίσω εγώ;;;
Όταν το + ή το - βρίσκεται αριστερά από τον αριθμό είναι πάντα πρόσημο!
Για παράδειγμα
+ 5 - 3
- 10 + 2
4 - 8 (Υπενθύμιση! Μπροστά από το 4 κρύβεται το πρόσημο +.)
Ωραία μέχρι εδώ... Μπορεί, όμως, να δούμε και αυτό...

-2 + (+4)
-5 + (-12)
Δε χρειάζεται πανικός... όπως είπαμε τα + και - που βρίσκονται αριστερά του αριθμού είναι τα πρόσημα (ροζ χρώμα).
 -2 + (+4)
-2 + (+4)
-5 + (-12)
Και τα + που μένουν τι είναι;
Το σύμβολο της πράξης (πορτοκαλί χρώμα)!
-2 + (+4)
-5 + (-12)
Α! Ωραία! Εύκολο και αυτό! Τώρα θα κάνω πρόσθεση, αλλά ποιο πρόσημο θα επιλέξω...;
Και τώρα αρχίζουν τα ωραία... Δεν είναι το σύμβολο της πράξης που καθορίζει την πράξη που θα κάνω, αλλά τα πρόσημα!!!!!

Πριν ξεκινήσει ο πανικός, ας δούμε μια ιστορία για ιππότες και δράκους.
Το παρακάτω διαδραστικό βίντεο αποτελεί μια ενδιαφέρουσα εισαγωγή στις πράξεις με ρητούς αριθμούς. Μέσα από ένα ευχάριστο, δημιουργικό και διαδραστικό τρόπο επιδιώκεται η κατανόηση, η εκμάθηση και η εφαρμογή του τρόπου που κάνουμε πράξεις με ρητούς αριθμούς.
Οδηγίες:
Στα κενά που εμφανίζονται πρέπει να συμπληρώσετε αριθμό και χρώμα. Για παράδειγμα "2 κόκκινοι", "3 μπλε", "κανένας" κλπ.
Καλή σας απόλαυση...
Σίγουρα οι ρητοί ήρθαν να αναστατώσουν τη "μαθηματική ζωή" μας. Ωστόσο, δεν πρέπει να το βάζουμε κάτω! Έτσι και αλλιώς τα μαθηματικά είναι θέμα εξάσκησης.

Το παρακάτω φύλλο εργασιών περιλαμβάνει ασκήσεις για εξάσκηση πάνω στην πρόσθεση των ρητών. Αφοπλιστείτε με υπομονή και πάμε!!!
Updated on Oktober 2, 2024
Κεφάλαιο 7 – Ρητοί Αριθμοί
Καλώς ήρθατε στον κόσμο των ρητών! Πρόκειται για ένα πολύ ιδιαίτερο ταξίδι, καθώς αυτή η νέα έννοια θα ανατρέψει κάποιες αρχές που είχαμε μάθει στο Δημοτικό.

Κάποιες φορές μπορεί να μπερδέψουμε το δρόμο μας ή να δυσκολευτούμε, αλλά δεν θα το βάλουμε κάτω! Αργά ή γρήγορα θα βρούμε το σωστό μονοπάτι που θα μας οδηγήσει στο δρόμο της επιτυχίας των μαθηματικών!
Τα αναμενόμενα μαθησιακά αποτελέσματα, μετά τη μελέτη της ενότητας είναι:
- να αναγνωρίζετε τους ρητούς αριθμούς και να τους διακρίνετε σε επιμέρους κατηγορίες (θετικοί, αρνητικοί, ομόσημοι, ετερόσημοι, αντίθετοι)
- να τοποθετείτε τους ρητούς στην ευθεία των πραγματικών αριθμών
- να συγκρίνετε ρητούς αριθμούς
- να κάνετε πράξεις με ρητούς αριθμούς.
Καλό ταξίδι !!!
7.1 Θετικοί και Αρνητικοί Αριθμοί (Ρητοί αριθμοί) – Η ευθεία των ρητών –Τετμημένη σημείου
7.2 Απόλυτη τιμή ρητού – Αντίθετοι ρητοί – Σύγκριση ρητών
7.3 Πρόσθεση ρητών αριθμών
7.4 Αφαίρεση ρητών αριθμών
7.5 Πολλαπλασιασμός ρητών αριθμών
7.6 Διαίρεση ρητών αριθμών
7.7 Δεκαδική Μορφή Ρητών Αριθμών
7.8. Δυνάμεις Ρητών Αριθμών με εκθέτη φυσικό
Δυνάμεις Ρητών Αριθμών με εκθέτη φυσικό
7.9. Δυνάμεις Ρητών Αριθμών με εκθέτη ακέραιο
Posted on September 16, 2024
Διδακτέα Ύλη Μαθηματικών Β‘ Γυμνασίου
Α΄Μέρος - ΆΛΓΕΒΡΑ 

Από το βιβλίο «Μαθηματικά Α΄ Γυμνασίου» των Ιωάννη Βανδουλάκη, Χαράλαμπου Καλλιγά, Νικηφόρου Μαρκάκη, Σπύρου Φερεντίνου:
Κεφ. 7ο: Θετικοί και Αρνητικοί Αριθμοί
7.7 Δεκαδική μορφή ρητών αριθμών
7.8 Δυνάμεις ρητών αριθμών με εκθέτη φυσικό
7.9 Δυνάμεις ρητών αριθμών με εκθέτη ακέραιο

Από το βιβλίο «Μαθηματικά Β΄ Γυμνασίου» των Παναγιώτη Βλάμου, Παναγιώτη Δρούτσα, Γεωργίου Πρέσβη, Κωνσταντίνου Ρεκούμη:
Κεφ. 1ο: Εξισώσεις - Ανισώσεις
1.1 Η έννοια της μεταβλητής – Αλγεβρικές παραστάσεις
1.2 Εξισώσεις α’ βαθμού
1.4 Επίλυση προβλημάτων με τη χρήση εξισώσεων
Κεφ. 2ο: Πραγματικοί Αριθμοί
2.1 Τετραγωνική ρίζα θετικού αριθμού
2.2 Άρρητοι αριθμοί – Πραγματικοί αριθμοί
2.3 Προβλήματα
Κεφ. 3ο: Συναρτήσεις
3.1 Η έννοια της συνάρτησης
3.2 Καρτεσιανές συντεταγμένες – Γραφική παράσταση συνάρτησης (χωρίς τις εφαρμογές 2 και 3).
3.3 Η συνάρτηση y=αx
3.4 Η συνάρτηση y=αx+β ( χωρίς τις υποπαραγράφους: «Η εξίσωση της μορφής «αx+βy=γ» και «Σημεία τομής της ευθείας αx+βy=γ με τους άξονες»).
3.5 Η συνάρτηση y=α/x – Η υπερβολή
Κεφ. 4ο: Περιγραφική Στατιστική
4.1 Βασικές έννοιες της Στατιστικής: Πληθυσμός – Δείγμα
4.2 Γραφικές Παραστάσεις
4.5 Μέση τιμή – Διάμεσος (χωρίς την υποπαράγραφο: “Μέση τιμή ομαδοποιημένης κατανομής“)
Β' Μέρος - ΓΕΩΜΕΤΡΙΑ

Κεφ. 1ο: Εμβαδά Επίπεδων Σχημάτων – Πυθαγόρειο Θεώρημα
1.1 Εμβαδόν επίπεδης επιφάνειας
1.2 Μονάδες μέτρησης επιφανειών
1.3 Εμβαδά επίπεδων σχημάτων
1.4 Πυθαγόρειο θεώρημα
Κεφ. 2ο: Τριγωνομετρία – Διανύσματα
2.1 Εφαπτομένη οξείας γωνίας
2.2 Ημίτονο και συνημίτονο οξείας γωνίας ( χωρίς την παρατήρηση β της σελίδας 143 )
Κεφ. 3ο: Μέτρηση Κύκλου
3.1 Εγγεγραμμένες γωνίες
3.2 Κανονικά πολύγωνα
3.3 Μήκος κύκλου
3.5 Εμβαδόν κυκλικού δίσκου
Κεφ. 4ο: Γεωμετρικά Στερεά – Μέτρηση Στερεών
4.2 Στοιχεία και εμβαδόν πρίσματος και κυλίνδρου
4.3 Όγκος πρίσματος και κυλίνδρου
4.4 Η πυραμίδα και τα στοιχεία της
4.6 Η σφαίρα και τα στοιχεία της
Posted on September 13, 2024
Διδακτέα Ύλη Μαθηματικών Α‘ Γυμνασίου

Από το βιβλίο "Μαθηματικά Α΄Γυμνασίου" των Ιωάννη Βανδουλάκη, Χαράλαμπου Καλλιγά, Νικηφόρου Μαρκάκη και Σπύρου Φερεντίνου.
Α' Μέρος- ΆΛΓΕΒΡΑ

Κεφ. 1ο: Οι φυσικοί αριθμοί
1.1 Φυσικοί αριθμοί – Διάταξη Φυσικών – Στρογγυλοποίηση
1.2 Πρόσθεση, αφαίρεση και πολλαπλασιασμός φυσικών αριθμών
1.3 Δυνάμεις φυσικών αριθμών
1.4 Ευκλείδεια διαίρεση – Διαιρετότητα
1.5 Χαρακτήρες διαιρετότητας – Μ.Κ.Δ. – Ε.Κ.Π. – Ανάλυση αριθμού σε γινόμενο πρώτων
παραγόντων
Κεφ. 2ο: Τα κλάσματα
2.1 Η έννοια του κλάσματος
2.2 Ισοδύναμα κλάσματα
2.3 Σύγκριση κλασμάτων
2.4 Πρόσθεση και Αφαίρεση κλασμάτων
2.5 Πολλαπλασιασμός κλασμάτων
2.6 Διαίρεση κλασμάτων
Κεφ. 3ο: Δεκαδικοί αριθμοί
3.1 Δεκαδικά κλάσματα, Δεκαδικοί αριθμοί, Διάταξη δεκαδικών αριθμών, Στρογγυλοποίηση
3.5 Μονάδες μέτρησης
Κεφ. 4ο: Εξισώσεις και προβλήματα
4.1 Η έννοια της εξίσωσης – Οι εξισώσεις: α+x=β , x-α=β , α-x=β , αx=β, α:x=β και x:α=β (χωρίς τις έννοιες της ταυτότητας και της αδύνατης εξίσωσης )
4.2 Επίλυση προβλημάτων
4.3 Παραδείγματα επίλυσης προβλημάτων
Κεφ. 5ο: Ποσοστά
5.1 Ποσοστά
5.2 Προβλήματα με ποσοστά
Κεφ. 7ο: Θετικοί και Αρνητικοί Αριθμοί
7.1 Θετικοί και Αρνητικοί Αριθμοί (Ρητοί αριθμοί) – Η ευθεία των ρητών –Τετμημένη σημείου
7.2 Απόλυτη τιμή ρητού – Αντίθετοι ρητοί – Σύγκριση ρητών
7.3 Πρόσθεση ρητών αριθμών
7.4 Αφαίρεση ρητών αριθμών
7.5 Πολλαπλασιασμός ρητών αριθμών
7.6 Διαίρεση ρητών αριθμών
Β΄ Μέρος - ΓΕΩΜΕΤΡΙΑ
Κεφ. 1ο: Βασικές γεωμετρικές έννοιες
1.1 Σημείο – Ευθύγραμμο τμήμα – Ευθεία – Ημιευθεία – Επίπεδο – Ημιεπίπεδο
1.2 Γωνία – Γραμμή – Επίπεδα σχήματα – Ευθύγραμμα σχήματα – Ίσα σχήματα
1.3 Μέτρηση, σύγκριση και ισότητα ευθυγράμμων τμημάτων – Απόσταση σημείων – Μέσο ευθυγράμμου τμήματος
1.4 Πρόσθεση και αφαίρεση ευθυγράμμων τμημάτων
1.5 Μέτρηση, σύγκριση και ισότητα γωνιών – Διχοτόμος γωνίας
1.6 Είδη γωνιών – Κάθετες ευθείες
1.7 Εφεξής και διαδοχικές γωνίες – Άθροισμα γωνιών
1.8 Παραπληρωματικές και Συμπληρωματικές γωνίες – Κατακορυφήν γωνίες
1.9 Θέσεις ευθειών στο επίπεδο
1.10 Απόσταση σημείου από ευθεία – Απόσταση παραλλήλων
1.11 Κύκλος και στοιχεία του κύκλου
1.12 Επίκεντρη γωνία
1.13 Θέσεις ευθείας και κύκλου
Κεφ. 2ο: Συμμετρία
2.1 Συμμετρία ως προς άξονα
2.2 Άξονας συμμετρίας
2.3 Μεσοκάθετος ευθυγράμμου τμήματος
2.4 Συμμετρία ως προς σημείο
2.5 Κέντρο συμμετρίας
2.6 Παράλληλες ευθείες που τέμνονται από μία άλλη ευθεία
Κεφ. 3ο: Τρίγωνα – Παραλληλόγραμμα – Τραπέζια
3.1 Στοιχεία τριγώνου – Είδη τριγώνων
3.2 Άθροισμα γωνιών τριγώνου – Ιδιότητες ισοσκελούς τριγώνου
3.3 Παραλληλόγραμμο – Ορθογώνιο – Ρόμβος – Τετράγωνο – Τραπέζιο – Ισοσκελές τραπέζιο
3.4 Ιδιότητες Παραλληλογράμμου – Ορθογωνίου – Ρόμβου – Τετραγώνου – Τραπεζίου – Ισοσκελούς τραπεζίου
Updated on Dezember 10, 2023
Προβλήματα με Εξισώσεις

Τα προβλήματα αποτελούν πάντα το μεγαλύτερο πρόβλημα στα μαθηματικά! Οι δυσκολίες που προκύπτουν σχετίζονται, κυρίως, με την κωδικοποίηση του προβλήματος, δηλαδή τη μετάφρασή του σε μαθηματική ορολογία. Για το λόγο αυτό, για να προχωρήσουμε στην ενότητα αυτή, πρέπει να έχουμε κατανοήσει καλά τις ενότητες:
που περιγράφτηκαν στην Ενότητα 4.1.
Βήματα για την Επίλυση Προβλημάτων με τη χρήση Εξισώσεων
Η διαδικασία επίλυσης προβλημάτων θα γίνει σίγουρα πιο εύκολη, αν ακολουθήσετε τα παρακάτω βήματα:
- Διαβάζουμε καλά το πρόβλημα, όσες φορές χρειαστεί, μέχρι να το κατανοήσουμε. Ποτέ δε ξεκινάμε να λύσουμε ένα πρόβλημα, αν δεν το έχουμε κατανοήσει πλήρως!
- Προσδιορίζουμε το ζητούμενο του προβλήματος και το εκφράζουμε με μια μεταβλητή (συνήθως το x). Αν το πρόβλημα έχει περισσότερα από ένα ζητούμενα επιλέγουμε αυτό που θα συμβολίσουμε με x.
- Εκφράζουμε όλα τα στοιχεία του προβλήματος με τη βοήθεια της μεταβλητής. Σε αυτό το βήμα πρέπει να ξέρουμε να κάνουμε καλή μετάφραση - κωδικοποίηση.
- Σχηματίζουμε μια εξίσωση από τα δεδομένα του προβλήματος.
- Επιλύουμε την εξίσωση του προβλήματος. Σε αυτό το βήμα πρέπει να γνωρίζουμε να λύνουμε τις εξισώσεις διαισθητικά.
- Επαληθεύουμε τη λύση που βρήκαμε. Σε πρώτη φάση πρέπει να ελέγξουμε αν η απάντηση που βρήκαμε είναι λογική (π.χ. δε μπορεί η ηλικία της μαμάς να είναι 20 και του παιδιού 45!) και στη συνέχεια να κάνουμε αντικατάσταση της τιμής που βρήκαμε στην αρχική για να δούμε αν την επαληθεύει.
Νομίζω ότι όλα φαίνονται ωραία και κατανοητά, αλλά σίγουρα έχετε την απορία "Πώς εφαρμόζονται όλα αυτά στην πράξη;"
Για να κατανοήσετε τη διαδικασία επίλυσης προβλημάτων με εξισώσεις παρακολουθήστε τα παρακάτω βίντεο. Πρόκειται για δύο παραδείγματα που δείχνουν όλη τη διαδικασία επίλυσης ενός προβλήματος με εξισώσεις.
Παράδειγμα 1
Πηγή: PublicSchooltv (2012, Φεβρουάριος 22). 4.2 Επίλυση προβλημάτΩν Παράδειγμα 1 α' γυμνασίου [βίντεο]. YouTube. Ανακτήθηκε από https://www.youtube.com/watch?v=cXN1MT-j7-g
Πάμε να κάνουμε και το αντίστροφο; Δηλαδή, αν μου δώσουν μια εξίσωση, μπορώ να φτιάξω ένα δικό μου πρόβλημα και να το λύσω;
Παράδειγμα 2
Πηγή: PublicSchooltv (2012, Φεβρουάριος 22). 4.2 Επίλυση προβλημάτΩν Παράδειγμα 2 α' γυμνασίου [βίντεο]. YouTube. Ανακτήθηκε από https://www.youtube.com/watch?v=cXN1MT-j7-g
Παρατήρηση:
Στα δύο παραδείγματα, μήπως διαπιστώσατε να λείπει κάποιο βήμα από τη διαδικασία επίλυσης;
Είναι το τελευταίο, η επαλήθευση.
Αυτό συμβαίνει για δύο λόγους:
- η επαλήθευση μπορεί να γίνει με το μυαλό και δεν είναι υποχρεωτικό να φαίνεται στη διαδικασία
- δεν κάνουμε επαλήθευση.
Αν και η επαλήθευση δεν είναι υποχρεωτική (εκτός και αν το ζητάει η άσκηση), πρέπει να γίνεται, καθώς είναι εκείνη που θα μας κατευθύνει να συνειδητοποιήσουμε την ύπαρξη λάθους, να το εντοπίσουμε και να το διορθώσουμε.
Γράψτε μου στα σχόλια, εσείς μέχρι τώρα κάνατε επαλήθευση στα προβλήματα;
Τώρα πλέον είμαστε έτοιμοι να λύσουμε τα δικά μας προβλήματα! Προσπαθήστε να λύσετε τα Προβλήματα 1, 2, 3, 5, 6 και 7 από το Σχολικό Βιβλίο Α' Γυμνασίου στο κεφάλαιο 4.3.
Σχόλιο
Δυστυχώς τα προβλήματα στα μαθηματικά αποτελούσαν και συνεχίζουν να αποτελούν το μεγαλύτερο εφιάλτη των μαθητών. Το πιο συνηθισμένο ερώτημα των μαθητών, όταν μαθαίνουν ένα νέο εργαλείο, είναι: "Και που θα μου χρειαστεί εμένα αυτό;". Η απάντηση, λοιπόν, είναι ότι όλα τα μαθηματικά εργαλεία τα χρησιμοποιούμε για να λύνουμε προβλήματα (όχ μόνο οικονομικά). Και είναι σημαντικό να μάθουμενα λύνουμε προβλήματα, καθώς όλη μας η ζωή είναι γεμάτη από αυτά.
Είναι πολύ σημαντικό να κατανοήσετε τη σπουδαιότητα των μαθηματικών προβλημάτων. Μόνο έτσι θα θελήσετε να ασχοληθείτε πραγματικά μαζί τους, θα μπείτε στον κόσμο τους και θα αφεθείτε στη μαγεία τους. Για το σκοπό αυτό, αφιερώστε λίγο χρόνο να καταγράψετε την άποψή σας για τα μαθηματικά προβλήματα, καθώς και να διαβάσετε τις απόψεις των υπόλοιπων συμμετεχόντων στον εξής σύνδεσμο Σημασία Μαθηματικών Προβλημάτων.
Αφοπλιστείτε με υπομονή και πάμε να κατανοήσουμε τον κόσμο!!!