Updated on Januar 5, 2025
Α.3.2 Καρτεσιανές Συντεταγμένες – Γραφική Παράσταση Συνάρτησης
Οι συντεταγμένες είναι μια έννοια που έχετε έρθει σε επαφή ήδη από την Α' Γυμνασίου, στο μάθημα της Γεωγραφίας, στο οποίο έχουν και μεγάλη εφαρμογή. Εδώ θα τις γνωρίσουμε ξανά από την αρχή και θα κάνουμε κάποιες βασικές παρατηρήσεις. Μπορεί να φαίνεται αρκετά εύκολο ως μάθημα, αλλά κρύβει και αυτό τις δυσκολίες του. Γι' αυτό το λόγο θα τις προσεγγίσουμε διερευνητικά.
https://www.geogebra.org/m/VUnV62vT (δημιουργός σελίδας e-arsakeio)
Στον παραπάνω σύνδεσμο υπάρχουν δραστηριότητες και πειράματα που θα μας βοηθήσουν να κατανοήσουμε τη θεωρία με πιο δημιουργικό και ευχάριστο τρόπο. Υπάρχουν αναλυτικές οδηγίες κάτω από κάθε δραστηριότητα ή πείραμα. Γι' αυτό σας προτείνω να μπείτε στη σελίδα, να ασχοληθείτε με τις δραστηριότητες και στο τέλος να ελέγξετε τις γνώσεις που αποκτήσατε με τη θεωρία που ακολουθεί.
Updated on Januar 4, 2025
Α.3.1. Η έννοια της συνάρτησης
Αυτό που μας έχει δυσκολέψει μέχρι τώρα στο ταξίδι μας ήταν η έννοια της μεταβλητής και η διαχείρισή της. Και επειδή είμαστε φοβεροί ταξιδιώτες, πάμε να ζήσουμε πιο δύσκολες περιπέτειες, εξερευνώντας την έννοια της συνάρτησης.
Θα ξεκινήσουμε απευθείας με βουτιά στα βαθιά και συγκεκριμένα στον ορισμό της συνάρτησης.
Ορισμός:
Συνάρτηση είναι μια διαδικασία κατά την οποία κάθε τιμή της μεταβλητής x αντιστοιχίζεται σε μία μόνο τιμή της μεταβλητής y.

Είναι λογικό να μην καταλάβατε τίποτα... Πάμε να τα δούμε μαζί αναλυτικά και θα γίνουν όλα κατανοητά!
Η έννοια της συνάρτησης
Για να κατανοήσουμε την έννοια της μεταβλητής, θα μεταφερθούμε μέχρι το Colorado και το εικονικό εργαστήριο Phet (https://phet.colorado.edu/).
Η συνάρτηση είναι μια μηχανή, όπως αυτή που βλέπετε παρακάτω, στην οποία κάνεις μια εισαγωγή και παίρνεις ένα αποτέλεσμα.
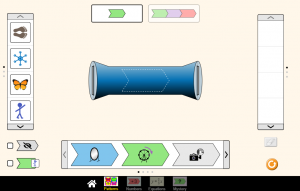
Ας επιλέξουμε, για παράδειγμα, ο μηχανισμός να είναι ο καθρέπτης. Αν επιλέξουμε ως είσοδο τις πατούσες, παρατηρούμε ότι ως αποτέλεσμα βγαίνουν οι πατούσες όπως θα τις βλέπαμε τις τοποθετούσαμε μπροστά σε έναν καθρέπτη.
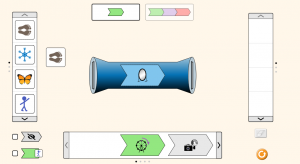

Αυτό σημαίνει ότι το αποτέλεσμα της μηχανής μπορεί να είναι διαφορετικό από αυτό που εισάγουμε. Μπορεί, όμως, να είναι και το ίδιο.
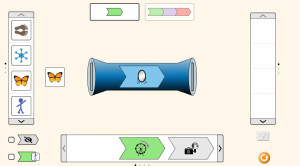
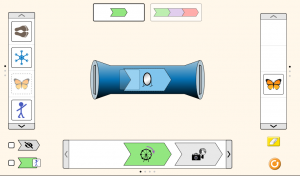
Εδώ βάλαμε την πεταλούδα και μετά το καθρέφτισμα βγάλαμε το ίδιο αποτέλεσμα.
Επίσης, η μηχανή (δηλαδή η συνάρτηση) μπορεί να είναι πιο περίπλοκη, όπως στο παρακάτω παράδειγμα.
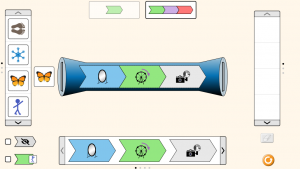
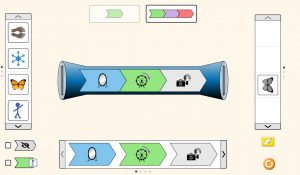
Εδώ η πεταλούδα καθρεφτίστηκε, περιστράφηκε και έγινε ασπρόμαυρη.
Και θα μου πείτε... και τι σχέση έχουν όλα αυτά με τα μαθηματικά;
Η μηχανή (συνάρτηση) δεν σχετίζεται μόνο με πατούσες και πεταλούδες, αλλά και με αριθμούς.
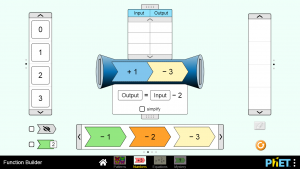
Ο μηχανισμός της συνάρτησης εδώ είναι, στον αριθμό που θα εισαχθεί στη μηχανή, να προσθέσεις 1 και στη συνέχεια να αφαιρέσεις το 3.
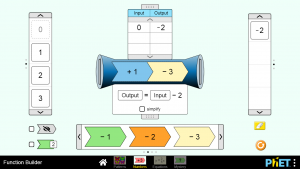
Αν εισάγουμε τον αριθμό 0, παρατηρούμε ότι το αποτέλεσμα βγαίνει -2, καθώς
0+1-3=-2
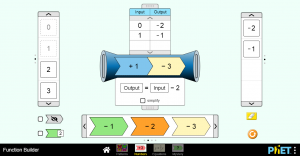
Αν εισάγουμε τον αριθμό 1 το αποτέλεσμα βγαίνει -1, καθώς
1+1-3=+2-3=-1
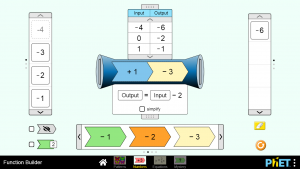
Τέλος, αν βάλουμε τον αριθμό -4, το αποτέλεσμα βγαίνει -6, καθώς
-4+1-3=-7+1=-6.
Μπορείτε να μπείτε στο σύνδεσμο https://phet.colorado.edu/sims/html/function-builder/latest/function-builder_all.html να επιλέξετε την επιλογή Numbers και να πειραματιστείτε πάνω στο μηχανισμό της συνάρτησης.
Πάμε να δούμε τώρα τη σχέση που έχουν όλα αυτά που είδαμε με τον ορισμό.
- Όπως είδαμε στις εικόνες σε κάθε συνάρτηση υπάρχει η είσοδος και το αποτέλεσμα. Η είσοδος είναι ο αριθμός x και το αποτέλεσμα είναι ο αριθμός y.
- Για να πάρει μπρος η μηχανή (συνάρτηση) πρέπει να έχει οπωσδήποτε μια είσοδο. Αυτό σημαίνει η φράση "κάθε μεταβλητή x".
- Επίσης, η μηχανή (συνάρτηση) βγάζει ένα αποτέλεσμα κάθε φορά. Αυτό σημαίνει η έκφραση "σε μία μόνο τιμή της μεταβλητής y".
Με πολύ απλά λόγια, η συνάρτηση είναι μια αντιστοίχηση, κατά την οποία επιλέγω ένα x και το αντιστοιχίζω σε ένα μόνο αριθμό y.
Και, όπως καταλαβαίνετε, η δυσκολία της είναι ότι εδώ έχουμε να διαχειριστούμε 2 μεταβλητές!!!
Τύπος συνάρτησης
Και θα μου πείτε και πάλι, ωραία όλα αυτά... αλλά τη μηχανή θα μου τη δίνουν έτοιμη ή θα πρέπει να τη φτιάξω εγώ;
Η απάντηση είναι ... εξαρτάται από την άσκηση!
- Η πιο απλή περίπτωση είναι να δίνεται ο τύπος της συνάρτησης.
Για παράδειγμα, έστω ότι δίνεται η συνάρτηση y=2x και ο παρακάτω πίνακας.
| x | 0 | -1 | |
| y | 4 |
Για να συμπληρώσουμε τα κελιά του πίνακα που είναι κενά, θα κάνουμε αντικατάσταση του αριθμού που μας δίνεται, στη συνάρτηση.
Προσοχή! Πρέπει να προσέχουμε αν ο αριθμός πρέπει να μπει στη θέση του x ή του y.
Στο παράδειγμά μας, η πάνω σειρά είναι οι τιμές του x και η κάτω σειρά είναι οι τιμές του y.
| x | 0 | -1 | |
| y | 4 |
Άρα για x=0, θα κάνω αντικατάσταση στη συνάρτηση y=2x όπου x το 0 και θα κάνω τις πράξεις, δηλαδή
y=2x
y=2•0
y=0
| x | 0 | -1 | |
| y | 0 | 4 |
Για x=-1 έχουμε
y=2x
y=2•(-1)
y=-2
| x | 0 | -1 | |
| y | 0 | -2 | 4 |
Για y=4 έχουμε
y=2x
4=2x
4/2=2x /2
2=x
| x | 0 | -1 | 2 |
| y | 0 | -2 | 4 |
Σε αυτό το σημείο, μπορείτε να ασχοληθείτε με την Ερώτηση Κατανόησης 5 στη σελίδα 57 του σχολικού βιβλίου και τις ασκήσεις 1, 2 και 7 στην ίδια σελίδα.
- Η πιο δύσκολη περίπτωση είναι να πρέπει να βρούμε εμείς τον τύπο.
Σε αυτήν την περίπτωση θα ήθελα να ανατρέξετε στην έννοια της μεταβλητής και να θυμηθείτε πώς κάναμε τη "μετάφραση" στα μαθηματικά. Οι πληροφορίες που χρειάζεστε βρίσκονται στον παρακάτω σύνδεσμο.
Τα μαθηματικά, μια παγκόσμια γλώσσα

Υπενθύμιση
Σε αυτό το σημείο θα ήθελα να θυμηθούμε τους τύπους που συνδέουν την αύξηση, τη μείωση, την αρχική και την τελική τιμή, όταν έχουμε ποσοστά.
Όταν έχουμε αύξηση:
Αύξηση = ποσοστό • Αρχική Τιμή
Τελική Τιμή = Αρχική Τιμή + ποσοστό • Αρχική Τιμή
Όταν έχουμε μείωση:
Μείωση = ποσοστό • Αρχική Τιμή
Τελική Τιμή = Αρχική Τιμή - ποσοστό • Αρχική Τιμή
Σε αυτό το σημείο, μπορείτε να κάνετε τις Ερωτήσεις Κατανόησης 1, 2, 3 και 4 στις σελίδες 56-57 του σχολικού βιβλίου, καθώς και τις ασκήσεις 3, 4, 5, 6 και 8 στη σελίδα 57 του σχολικού βιβλίου.
Σε αυτό το σημείο, μπορείτε να ασχοληθείτε με την Ερώτηση Κατανόησης 5 στη σελίδα 57 του σχολικού βιβλίου και τις ασκήσεις 1, 2 και 7 στην ίδια σελίδα.
- .
Updated on Januar 4, 2025
Α.2.3. Προβλήματα με ρίζες
Τα προβλήματα είναι πάντα... προβλήματα! Όπως είδατε στα προηγούμενα μαθήματα, η τετραγωνική ρίζα ενός αριθμού είναι ένας αριθμός με τις δικές του ιδιότητες. Ωστόσο, ως αριθμός, μπορεί κανείς να το συναντήσει οπουδήποτε, ακόμα και στα προβλήματα!
 Σε αυτό το σημείο, ας θυμηθούμε τη διαδικασία που ακολουθούμε για να λύσουμε ένα πρόβλημα.
Σε αυτό το σημείο, ας θυμηθούμε τη διαδικασία που ακολουθούμε για να λύσουμε ένα πρόβλημα.
- Διαβάζουμε το πρόβλημα καλά και όσες φορές χρειαστεί μέχρι να το καταλάβουμε.
- Καταγράφουμε τα δεδομένα και τα ζητούμενα.
- Σχεδιάζουμε τον τρόπο επίλυσης του προβλήματος.
- Λύνουμε το πρόβλημα.
- Ελέγχουμε και επαληθεύουμε τη λύση.
Αφοπλιστείτε με αρκετή υπομονή και επιμονή και πάμε!!!
Στον παρακάτω σύνδεσμο υπάρχει ένα φύλλο εργασιών με προβλήματα.

Updated on Dezember 28, 2024
Α.2.2. Άρρητοι Αριθμοί – Πραγματικοί Αριθμοί
Στο προηγούμενο μάθημα γνωρίσαμε την τετραγωνική ρίζα και κάποιες βασικές ιδιότητές της. Σε αυτό το μάθημα θα συνεχίσουμε με τις ιδιότητες των ριζών. Επίσης, θα γνωρίσουμε τα σύνολα των αριθμών και θα εντάξουμε τις ρίζες μέσα σε αυτά. Τέλος, θα μάθουμε να υπολογίζουμε τις ρίζες με αριθμομηχανή και με προσέγγιση. Αφοπλιστείτε με υπομονή και πάμε!!!
Μέχρι τώρα έχουμε δει ρίζες που μπορούμε να τις υπολογίσουμε σύμφωνα με τον ορισμό. Δηλαδή να βρούμε έναν αριθμό που όταν τον υψώσουμε στο τετράγωνο να μας δίνει το υπόρριζο. Αυτό, όμως, γίνεται πάντα;
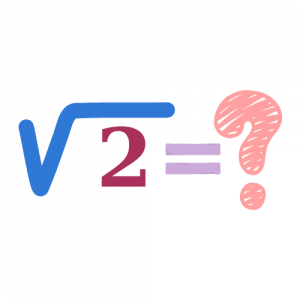
Όπως γνωρίζουμε, δεν υπάρχει αριθμός (φυσικός) που να τον υψώσουμε στο τετράγωνο και να μας κάνει 2.
Μήπως τότε το 2 δεν πρέπει να το βάζουμε στο υπόρριζο;
Φυσικά και μπορούμε! Οποιοσδήποτε θετικός αριθμός ή 0 μπορεί να μπει μέσα σε ρίζα.
Και τότε πώς υπολογίζεται;
Πάμε να δούμε μαζί...
Υπάρχουν δύο τρόποι για να υπολογίσουμε τέτοιες ρίζες.
Α' Τρόπος: Με αριθμομηχανή
Πατάμε στην αριθμομηχανή το σύμβολο της ρίζας και μετά τον αριθμό ή το αντίστροφο, ανάλογα με τη συσκευή / υπολογιστική μηχανή, που χρησιμοποιείτε.
Β' Τρόπος: Με χαρτί, μολύβι και υπομονή...
Για να καταλάβετε αυτόν τον τρόπο, παρακολουθήστε το παρακάτω βίντεο.
Πηγή: Haraldim1 (2016, Αύγουστος 17). Ρητή προσέγγιση τετραγωνικής ρίζας [βίντεο]. YouTube. Ανακτήθηκε από https://www.youtube.com/watch?v=S5-vu2Ascgo
Σύνολα Αριθμών
Φυσικοί αριθμοί είναι οι αριθμοί 0, 1, 2, 3, 4,....

Ακέραιοι αριθμοί είναι όλοι οι φυσικοί με τους αντίστοιχους αρνητικούς. Δηλαδή, ..., -3, -2, -1, 0, 1, 2, 3, ...

Ρητοί αριθμοί είναι όλοι οι αριθμοί που μπορούν να πάρουν τη μορφή κλάσματος. Σε αυτό το σύνολο ανήκουν:
- φυσικοί
- ακέραιοι
- περιοδικοί
- ρίζες που υπολογίζονται
- δεκαδικοί αριθμοί με πεπερασμένο πλήθος δεκαδικών ψηφίων
- κλάσματα
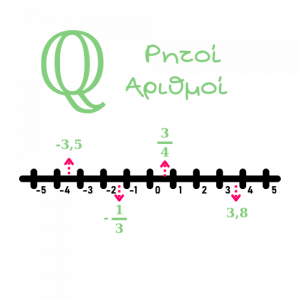
Άρρητοι Αριθμοί είναι οι αριθμοί που δεν είναι ρητοί, δηλαδή δε μπορούν να πάρουν τη μορφή κλάσματος. Σε αυτό το σύνολο ανήκουν:
- δεκαδικοί αριθμοί με άπειρο πλήθος δεκαδικών ψηφίων
- ρίζες που δεν υπολογίζονται
Πραγματικοί Αριθμοί είναι όλοι οι αριθμοί που γνωρίζουμε μέχρι τώρα και περιλαμβάνουν όλα τα παραπάνω σύνολα αριθμών (φυσικούς, ακεραίους, ρητούς και άρρητους).

Ιδιότητες Ριζών
Πάμε να δούμε και κάποιες άλλες ιδιότητες των ριζών, όπως είναι η σύγκριση ριζών, η πρόσθεση και η αφαίρεση άρρητων, η απλοποίηση ριζών κλπ. Η θεωρία βρίσκεται αναλυτικά στον παρακάτω σύνδεσμο. Στο πρώτο μέρος είναι η θεωρία με παραδείγματα και στο δεύτερο μέρος ασκήσεις για εμπέδωση και εξάσκηση.

Updated on Dezember 28, 2024
Α.2.1. Τετραγωνική Ρίζα θετικού αριθμού

Καλωσορίσατε στον κόσμο των ριζών. Είστε έτοιμοι να μάθουμε τις ρίζες μας;
Μα φυσικά δεν εννοώ το γενεαλογικό μας δέντρο!
Αλήθεια, έχετε παρατηρήσει ποτέ σε κάποια αριθμομηχανή το παρακάτω σύμβολο;

Αυτό είναι ένα καινούριο μαθηματικό σύμβολο που θα γνωρίσουμε στο κεφάλαιο αυτό. Είστε έτοιμοι για νέες γνωριμίες;

Ας ξεκινήσουμε να δούμε το σύμβολο αυτό και τον ορισμό του σχολικού βιβλίου.

Ορισμός:
Τετραγωνική ρίζα ενός θετικού αριθμού α, λέγεται ο θετικός αριθμός, ο οποίος όταν υψωθεί στο τετράγωνο, δίνει τον αριθμό α.
Η τετραγωνική ρίζα του α συμβολίζεται με √α.

Είμαι σίγουρη ότι δεν καταλάβατε τίποτα... και είναι απολύτως λογικό! Πάμε να δούμε μαζί κάποια παραδείγματα και θα δείτε ότι θα τα καταλάβετε όλα!!!

Προσοχή!
Ένα συχνό λάθος που γίνεται με τον υπολογισμό της τετραγωνικής ρίζας είναι η διαίρεση της υπόρριζης ποσότητας με το 2... Σε καμία περίπτωση δε διαιρούμε με το 2!
Ουσιαστικά, ψάχνουμε έναν αριθμό, που όταν τον υψώσουμε στο τετράγωνο, να μας δίνει την υπόρριζη ποσότητα.
Για να δούμε αν τα εμπεδώσαμε, πάμε να κάνουμε ένα μικρό quiz!

Υπολογισμός Τετραγωνικής Ρίζας
Ιδιότητες Τετραγωνικής Ρίζας
Οι ιδιότητες της τετραγωνικής ρίζας εμφανίζονται αναλυτικά στο παρακάτω σύνδεσμο. Το πρώτο μέρος περιλαμβάνει αναλυτικά τη θεωρία με παραδείγματα και το δεύτερο μέρος έχει ασκήσεις για εμπέδωση.

Updated on November 22, 2024
1.4 Πυθαγόρειο Θεώρημα
Αυτή τη χρονιά θα ασχοληθούμε αρκετά με τα τρίγωνα και κυρίως με τα ορθογώνια τρίγωνα. Πάμε να τα γνωρίσουμε λίγο καλύτερα;

Ορθογώνιο τρίγωνο ονομάζεται το τρίγωνο που έχει μια ορθή γωνία (δηλαδή μια γωνία 90º).
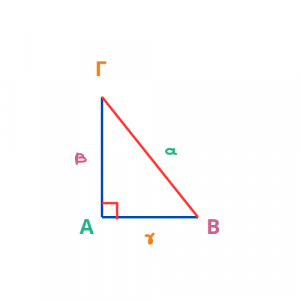 Υπενθυμίζουμε ότι το ορθογώνιο τρίγωνο έχει τρεις πλευρές, οι οποίες ονομάζονται με δύο τρόπους:
Υπενθυμίζουμε ότι το ορθογώνιο τρίγωνο έχει τρεις πλευρές, οι οποίες ονομάζονται με δύο τρόπους:
- από τα ευθύγραμμα τμήματα ΑΒ, ΑΓ και ΒΓ
- από την απέναντι γωνία, χρησιμοποιώντας το αντίστοιχο μικρό γράμμα, δηλαδή
-
- απέναντι από τη γωνία Α βρίσκεται η πλευρά α
- απέναντι από τη γωνία Β βρίσκεται η πλευρά β και
- απέναντι από τη γωνία Γ βρίσκεται η πλευρά γ.
-
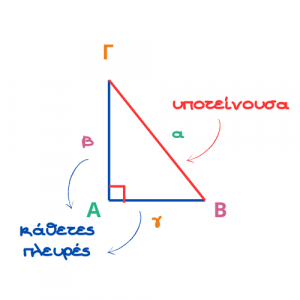
Η πλευρά που βρίσκεται απέναντι από την ορθή γωνία είναι η μεγαλύτερη πλευρά του ορθογωνίου τριγώνου και ονομάζεται υποτείνουσα.
Οι άλλες δύο πλευρές ονομάζονται κάθετες πλευρές.
Πυθαγόρειο Θεώρημα

Ένα από τα πιο αγαπητά θεωρήματα των μαθηματικών είναι το Πυθαγόρειο Θεώρημα. Και αν δε με πιστεύετε, δείτε το παρακάτω βίντεο.
Είναι τόσο διάσημο, που έχει γίνει και τραγούδι!!!!
"Σε κάθε ορθογώνιο τρίγωνο το άθροισμα των τετραγώνων των δύο κάθετων πλευρών είναι ίσο με το τετράγωνο της υποτείνουσας."
Και τι εννοεί ο Πυθαγόρας με αυτό;
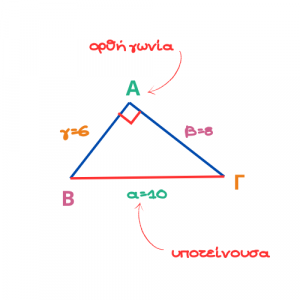
Παρατηρήστε την παρακάτω φωτογραφία.
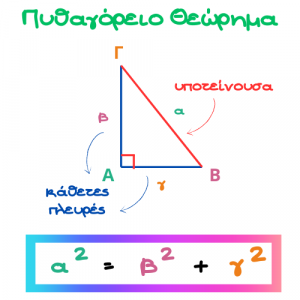
Το Πυθαγόρειο θεώρημα το χρησιμοποιούμε όταν γνωρίζουμε τις δύο πλευρές ενός ορθογωνίου τριγώνου και θέλουμε να βρούμε την τρίτη πλευρά.
Πάμε να το δούμε αναλυτικά μέσα από παραδείγματα.
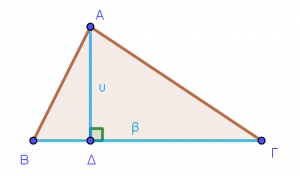
Α' Περίπτωση: Ξέρω τις δύο κάθετες πλευρές και ψάχνω να βρω την υποτείνουσα.
Παίρνω τον τύπο, κάνω αντικατάσταση στις κάθετες πλευρές και κάνω πράξεις.
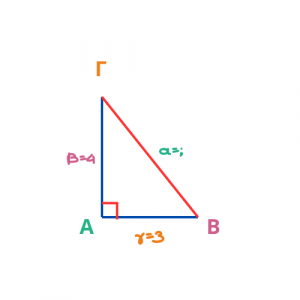 Εφαρμόζω Πυθαγόρειο Θεώρημα στο τρίγωνο ΑΒΓ και έχω:
Εφαρμόζω Πυθαγόρειο Θεώρημα στο τρίγωνο ΑΒΓ και έχω:
α2 = β2+γ2
ΒΓ2 = ΑΓ2+ΑΒ2
α2 = 42+32
α2 = 16+9
α2 = 25
α = 5
Β' Περίπτωση: Ξέρω την υποτείνουσα και τη μια κάθετη πλευρά και ψάχνω να βρω την άλλη κάθετη πλευρά.
Α' τρόπος: Παίρνω τον τύπο, κάνω αντικατάσταση την υποτείνουσα και λύνω εξίσωση.
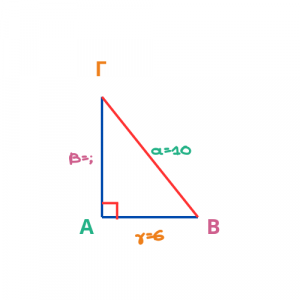
Εφαρμόζω Πυθαγόρειο Θεώρημα στο τρίγωνο ΑΒΓ και έχω:
α2 = β2+γ2
ΒΓ2 = ΑΓ2+ΑΒ2
102 = β2+62
100 = β2+36
β2 = 100-36
β2 = 64
β=8
Β' Τρόπος: Ξεκινάω από την πλευρά που ψάχνω, δηλαδή την κάθετη.
κάθετη2 = υποτείνουσα2 - κάθετη2
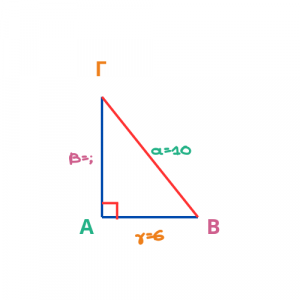
β2 = α2 - γ2
ΑΓ2 = ΒΓ2 - ΑΒ2
β2 = 102-62
β2=100-36
β2 = 64
β=8
Για να εμβαθύνουμε λίγο περισσότερο στο Πυθαγόρειο Θεώρημα, ας παρακολουθήσουμε το παρακάτω βίντεο, στο οποίο αναφέρονται δύο αποδείξεις του θεωρήματος.
Αντίστροφο Πυθαγορείου Θεωρήματος
"Αν σε ένα τρίγωνο, το τετράγωνο της μεγαλύτερης πλευράς είναι ίσο με το άθροισμα των τετραγώνων των δύο άλλων πλευρών, τότε η γωνία που βρίσκεται απέναντι από τη μεγαλύτερη πλευρά είναι ορθή."
Και σε τι μου χρησιμεύει αυτό;
Το αντίστροφο του Πυθαγορείου Θεωρήματος το χρησιμοποιούμε όταν γνωρίζουμε και τις 3 πλευρές ενός τριγώνου και θέλουμε να δείξουμε ότι το τρίγωνο είναι ορθογώνιο.
Ας δούμε ένα παράδειγμα:
Θέλουμε να εξετάσουμε αν το παρακάτω τρίγωνο είναι ορθογώνιο.
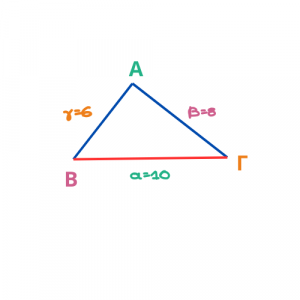
Εφαρμόζω Αντίστροφο Πυθαγόρειο Θεώρημα στο τρίγωνο ΑΒΓ και έχω:
Παίρνω τη μεγαλύτερη πλευρά στο τετράγωνο:
α2 = ΒΓ2=102=100
Παίρνω το άθροισμα των τετραγώνων των δύο άλλων πλευρών:
β2+γ2 = ΑΓ2+ΑΒ2 = 82+62 = 64+36=100
Άρα ισχύει α2 = β2+γ2. Οπότε το τρίγωνο είναι ορθογώνιο με υποτείνουσα την πλευρά α (τη μεγαλύτερη πλευρά) και ορθή γωνία τη γωνία Α.
Πάμε να τα συνοψίσουμε όλα αυτά στο παρακάτω βίντεο.
Updated on November 17, 2024
1.3 Εμβαδά Επίπεδων Σχημάτων
Αλήθεια, ξέρετε αν θέλετε να βάψετε το δωμάτιό σας, πόση μπογιά θα χρειαστείτε; Αν θέλετε να βάλετε πλακάκια σε ένα δωμάτιο; Αν θέλετε να κοστολογήσετε ένα χωράφι;

Και θα μου πείτε... είμαστε αρκετά μικροί για όλα αυτά. Αυτά θα τα κάνουν οι γονείς μας! Έχετε αναρωτηθεί ότι και οι γονείς σας μπορεί να μη ξέρουν και να χρειάζονται τη βοήθειά σας;
Όλα τα παραπάνω ερωτήματα σχετίζονται με την έννοια της επιφάνειας και του εμβαδού.
Πάμε να γνωρίσουμε τους τύπους για τα εμβαδά των γνωστών ευθύγραμμων σχημάτων.
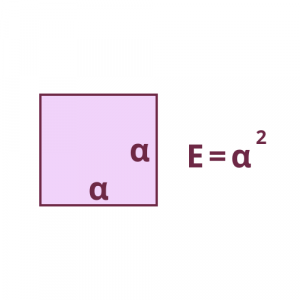
Τετράγωνο
Τετράγωνο είναι το τετράπλευρο που έχει όλες τις γωνίες ορθές και όλες τις πλευρές του ίσες.
Ο τύπος για το εμβαδόν του τετραγώνου είναι :
Ορθογώνιο
Ορθογώνιο είναι το τετράπλευρο που έχει τις απέναντι πλευρές του παράλληλες και τις γωνίες του ορθές.
Ο τύπος για το εμβαδόν του ορθογωνίου είναι:
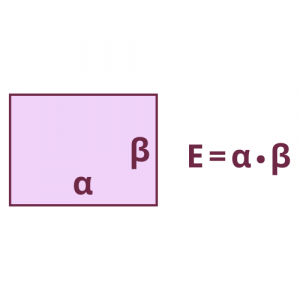
Δηλαδή, για να βρούμε το εμβαδόν του ορθογωνίου, πολλαπλασιάζουμε δύο διαδοχικές πλευρές του.
Εναλλακτικά, η μια πλευρά του ορθογωνίου μπορεί να θεωρηθεί ως βάση (β) και η άλλη ως ύψος (υ). Οπότε ο τύπος γίνεται:
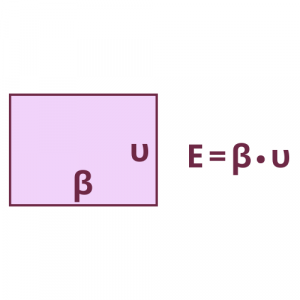
Παραλληλόγραμμο
Παραλληλόγραμμο είναι το σχήμα που έχει τις απέναντι πλευρές του παράλληλες.
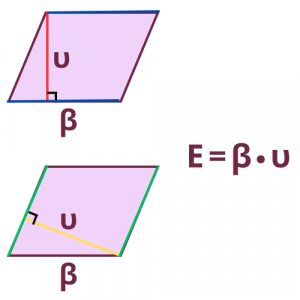
Ο τύπος για το εμβαδόν του παραλληλογράμμου είναι:
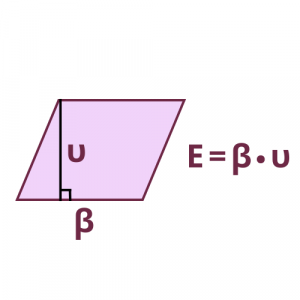
Παρατηρήσεις:
- Ως βάση του παραλληλογράμμου μπορούμε να πάρουμε οποιαδήποτε πλευρά του.
- Ο τύπος Ε=β•υ σημαίνει ότι πολλαπλασιάζω τη βάση με το αντίστοιχο ύψος.
- Οι παράλληλες πλευρές έχουν το ίδιο ύψος.
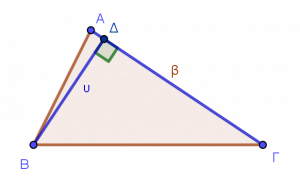
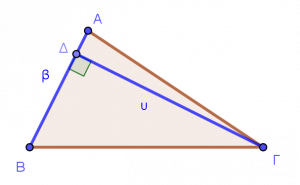
Τρίγωνο
Τρίγωνο είναι ένα σχήμα με τρεις πλευρές και τρεις γωνίες.
Ο τύπος για το εμβαδόν του τριγώνου είναι:
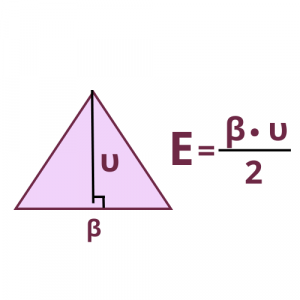
Παρατηρήσεις:
- Βάση μπορεί να θεωρηθεί οποιαδήποτε πλευρά του τριγώνου.
- Ως ύψος επιλέγουμε αυτό που αντιστοιχεί στη βάση που έχουμε επιλέξει.
- Ύψος ενός τριγώνου είναι το κάθετο ευθύγραμμο τμήμα που ξεκινάει από την κορυφή και καταλήγει στην απέναντι πλευρά του τριγώνου.
Τραπέζιο
Τραπέζιο ονομάζεται το σχήμα που έχει δύο μόνο απέναντι πλευρές παράλληλες.
Οι παράλληλες πλευρές ονομάζονται βάσεις του τραπεζίου.
Η μικρή παράλληλη πλευρά ονομάζεται μικρή βάση και συμβολίζεται με β, ενώ η μεγάλη παράλληλη πλευρά ονομάζεται μεγάλη βάση και συμβολίζεται με Β.
Ο τύπος για το εμβαδόν του τραπεζίου είναι:
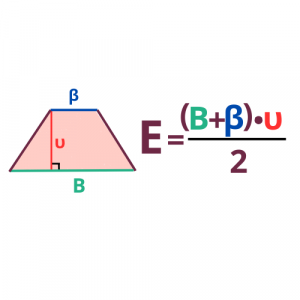
Παρατήρηση:
Ύψος είναι το κάθετο ευθύγραμμο τμήμα που έχει τα άκρα του στις παράλληλες πλευρές.
Για να εμβαθύνουμε λίγο παραπάνω στα εμβαδά, ας μελετήσουμε το παρακάτω αρχείο. Στο συγκεκριμένο αρχείο περιλαμβάνονται συνοπτικά οι τύποι, κάποιες βασικές παρατηρήσεις, μια βασική άσκηση, καθώς και πώς υπολογίζουμε το εμβαδόν ενός ακανόνιστου σχήματος.
 Ήρθε η ώρα της εξάσκησης. Το παρακάτω φύλλο εργασιών περιλαμβάνει ασκήσεις πάνω στα εμβαδά.
Ήρθε η ώρα της εξάσκησης. Το παρακάτω φύλλο εργασιών περιλαμβάνει ασκήσεις πάνω στα εμβαδά.
Updated on November 16, 2024
1.2 Μονάδες Μέτρησης Επιφανειών
Βασική μονάδα μέτρησης του εμβαδού είναι το τετραγωνικό μέτρο (m2). Φυσικά, δε χρησιμοποιούμε μόνο αυτό. Ανάλογα με το μέγεθος χρησιμοποιούμε πολλαπλάσια ή υποδιαιρέσεις του τετραγωνικού μέτρου.
Πάμε να τα γνωρίσουμε μαζί!

Πάμε τώρα να δούμε ποια είναι η σχέση που συνδέει όλες αυτές τις μονάδες.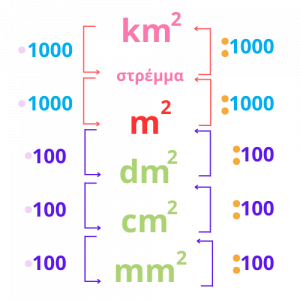
Όπως παρατηρείτε στη φωτογραφία, όταν βάλουμε τις μονάδες μέτρησης σε φθίνουσα σειρά (από τη μεγαλύτερη στη μικρότερη), δημιουργείται μια σκάλα.
Όταν κατεβαίνω τη σκάλα (δηλαδή πάω από μεγαλύτερες μονάδες μέτρησης σε μικρότερες) κάνω πολλαπλασιασμό.
Όταν ανεβαίνω τη σκάλα (δηλαδή πηγαίνω από μικρότερες μονάδες μέτρησης σε μεγαλύτερες) κάνω διαίρεση.
Επίσης, η σκάλα είναι ανομοιόμορφη καθώς στα πολλαπλάσια αντιστοιχεί ο αριθμός 1000, ενώ στις υποδιαιρέσεις αντιστοιχεί ο αριθμός 100.
Για να το καταλάβετε καλύτερα αυτό, παρατηρήστε την παρακάτω σκάλα.
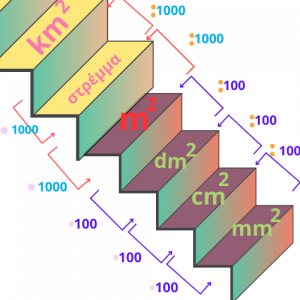
Για να καταλάβουμε πώς γίνονται οι μετατροπές από τη μια μονάδα στην άλλη, παρακολουθήστε το παρακάτω βίντεο.
 Ώρα να ελέγξουμε κατά πόσο μπορούμε να κάνουμε και μόνοι μας τις μετατροπές με ένα quizz!
Ώρα να ελέγξουμε κατά πόσο μπορούμε να κάνουμε και μόνοι μας τις μετατροπές με ένα quizz!
Updated on November 18, 2024
1.3 Μέτρηση, σύγκριση και ισότητα ευθυγράμμων τμημάτων – Απόσταση σημείων – Μέσο ευθυγράμμου τμήματος
Έχει τύχει ποτέ να μετρήσετε κάτι στη ζωή σας; Για παράδειγμα, ένα έπιπλο για να δείτε αν χωράει να περάσει από μια πόρτα, πόσο μακριά είναι το σπίτι σας από τη θάλασσα ή ακόμα και το ύψος σας;
Αν ναι, τι όργανα χρησιμοποιήσατε για να κάνετε τις μετρήσεις σας;
Υπάρχουν πολλά όργανα, με τα οποία μετράμε το μήκος και θα γνωρίσουμε μέσα από το βίντεο που ακολουθεί.
Πηγή: zouboulakis nikos (2018, Δεκέμβριος 31). Όργανα Μέτρησης Μήκους (nz) [βίντεο]. YouTube. Ανακτήθηκε από https://www.youtube.com/watch?v=aQB8X1_BYuk
Βασική μονάδα μέτρησης του μήκους είναι το μέτρο (m). Φυσικά, δε χρησιμοποιούμε μόνο αυτό. Ανάλογα με το μέγεθος χρησιμοποιούμε πολλαπλάσια ή υποδιαιρέσεις του τετραγωνικού μέτρου.
Πάμε να τα γνωρίσουμε μαζί!

Πάμε τώρα να δούμε ποια είναι η σχέση που συνδέει όλες αυτές τις μονάδες.
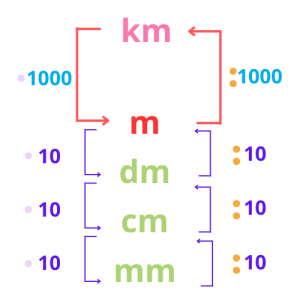
Όπως παρατηρείτε στη φωτογραφία, όταν βάλουμε τις μονάδες μέτρησης σε φθίνουσα σειρά (από τη μεγαλύτερη στη μικρότερη), δημιουργείται μια σκάλα.
Όταν κατεβαίνω τη σκάλα (δηλαδή πάω από μεγαλύτερες μονάδες μέτρησης σε μικρότερες) κάνω πολλαπλασιασμό.
Όταν ανεβαίνω τη σκάλα (δηλαδή πηγαίνω από μικρότερες μονάδες μέτρησης σε μεγαλύτερες) κάνω διαίρεση.
Επίσης, η σκάλα είναι ανομοιόμορφη καθώς στα πολλαπλάσια αντιστοιχεί ο αριθμός 1000, ενώ στις υποδιαιρέσεις αντιστοιχεί ο αριθμός 10.
Για να το καταλάβετε καλύτερα αυτό, παρατηρήστε την παρακάτω σκάλα.
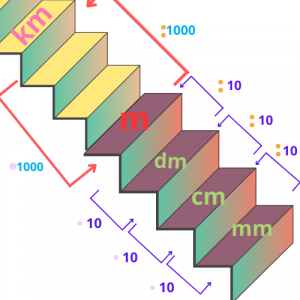
Για να καταλάβουμε πώς γίνονται οι μετατροπές από τη μια μονάδα στην άλλη, παρακολουθήστε το παρακάτω βίντεο.
 Ώρα να ελέγξουμε κατά πόσο μπορούμε να κάνουμε και μόνοι μας τις μετατροπές με ένα quiz!
Ώρα να ελέγξουμε κατά πόσο μπορούμε να κάνουμε και μόνοι μας τις μετατροπές με ένα quiz!
Απόσταση μεταξύ δύο σημείων
Απόσταση μεταξύ δύο σημείων Α και Β ονομάζεται το μήκος του ευθύγραμμου τμήματος που τα ενώνει και συμβολίζεται με ΑΒ ή (ΑΒ).
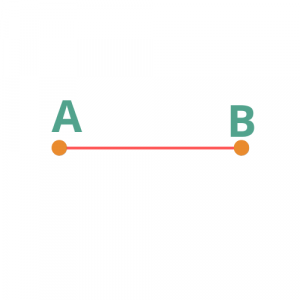
Μέσο ενός ευθύγραμμου τμήματος είναι ένα σημείο που ισαπέχει (απέχει την ίδια απόσταση) από τα άκρα του ευθύγραμμου τμήματος.

Για να βρούμε το μέσο ενός ευθύγραμμου τμήματος:
- Μετράμε το ευθύγραμμο τμήμα με το χάρακα.
- Διαιρούμε τον αριθμό που βρήκαμε δια 2.
- Βάζουμε το χάρακα πάνω στο ευθύγραμμο τμήμα και ξεκινάμε να μετράμε από το ένα άκρο, μέχρι να φτάσουμε στον αριθμό που βρήκαμε στη διαίρεση. Εκεί κάνουμε ένα σημείο και του δίνουμε ένα όνομα (αυτό που λέει η εκφώνηση ή αν δεν αναφέρεται στην εκφώνηση, επιλέγουμε όποιο θέλουμε εμείς).
Updated on November 3, 2024
Α.1.2. Εξισώσεις α‘ βαθμού
Ένα από τα μεγαλύτερα εργαλεία των μαθηματικών αποτελεί η εξίσωση.

- Εξίσωση είναι μια ισότητα που περιέχει έναν άγνωστο x.
Αλήθεια, μπορείτε να καταλάβετε τον παραπάνω ορισμό;

Για να σας βοηθήσω, ας μπούμε στο εικονικό εργαστήριο του Phet στον παρακάτω σύνδεσμο.
https://phet.colorado.edu/sims/html/equality-explorer/latest/equality-explorer_all.html
Στο περιβάλλον αυτό μπορείτε να δημιουργήσετε τις δικές σας εξισώσεις. Ιδιαίτερα στην καρτέλα Variables και Operations, μπορείτε να δημιουργήσετε τις δικές σας εξισώσεις, και να αλλάζετε τις τιμές του x (πάνω δεξιά), μέχρι να δείτε τη ζυγαριά να ισορροπεί, που σημαίνει ότι έχετε βρει τη λύση της εξίσωσης.
- Η δυσκολία εδώ και το σημείο που χρειάζεται μεγάλη προσοχή είναι να ξεχωρίσετε τις αλγεβρικές παραστάσεις από τις εξισώσεις.
Μια εξίσωση αποτελείται από δύο αλγεβρικές παραστάσεις. Η μια βρίσκεται δεξιά από το = και η άλλη αριστερά από το =.
Καθεμία από αυτές τις παραστάσεις αποτελούν τα μέλη της εξίσωσης.
| 2χ + 3 | = | χ - 7 - 5χ |
| Α΄μέλος | Β΄μέλος |
Διαδικασία Επίλυσης Εξισώσεων
Στον παρακάτω σύνδεσμο περιγράφεται αναλυτικά η διαδικασία που ακολουθούμε για την επίλυση των εξισώσεων Α' βαθμού.
Παρατηρήσεις:
Η σειρά των βημάτων που περιγράφονται στον παραπάνω σύνδεσμο δεν είναι αυστηρή. Ωστόσο, στο επίπεδο που είστε, καλό είναι να τα ακολουθείτε πιστά, ώστε να έχετε μικρότερες πιθανότητες για λάθη.